Как рассчитать чистый дисконтированный доход (формула)
Содержание:
- Чистый дисконтированный доход
- Инструменты дисконтирования: денежные потоки и ставка
- Пример
- Стоимость денег со временем изменяется
- Как пользоваться показателем IRR для оценки эффективности инвестиционного капитала проекта
- Рентабельность производства
- Практическое применение NPV (чистой текущей стоимости)
- Пример расчета
- Расчет и прогнозирование будущего денежного потока (CF) в Excel
- Необходимость расчёта
- Что такое чистый дисконтированный доход (ЧДД)
- Расчет чистого дисконтированного дохода
Чистый дисконтированный доход
ЧДД — это совокупность дисконтированных значений финансового роста и падения выбранного проекта на настоящий момент времени. В европейской практике данный параметр отображается при помощи аббревиатуры «NPV». Расшифровать данное сокращение можно как «Net Present Value». Довольно часто ЧДД именуют текущей стоимостью проекта.
Разница между доходом, полученным от инвестиционной деятельности и вложенным капиталом, является текущей стоимостью. Многие инвесторы используют этот критерий для проведения сравнения нескольких проектов по временным параметрам. На основе этого сравнения принимается решение о том, в какие проекты выгодно вложить имеющийся капитал.
Во время проведения анализа, инвестору следует учитывать такие показатели, как длительность цикла жизни выбранной сферы и величину дохода, получаемую за счет инвестиций. Помимо этого, следует учитывать срок вложения капитала. Использование рассматриваемого значения помогает удалить временные ограничения, для того, чтобы выявить размер дохода, который можно получить за определенный промежуток времени.
Обобщая все вышесказанное можно сделать вывод, что данный аналитический инструмент позволяет определить результативность инвестиционной деятельности. Применение ЧДД позволяет получить точную информацию о том, какой из проектов принесет большую прибыль. На основании данных расчетов выбирается один из бизнесов, доход которого превышает уровень выручки остальных компаний.
Инструменты дисконтирования: денежные потоки и ставка
В начале расчетов денежные потоки группируют в разрезе некоторых временных интервалов: год, квартал, месяц, а затем суммируют. Полученные величины могут быть с плюсом (поступления больше оттоков) или с минусом, убыточными (отток превышает сумму поступлений). В качестве денежного потока в расчетах могут считать:
-
чистый доход, равный поступившим доходам за вычетом расходов;
-
прибыль, рассчитываемая до исчисления налогов;
-
чистый поток наличности, из которого исключаются текущие затраты на содержание и реконструкцию объекта.
Вычисление ставки дисконтирования — наиболее ответственный момент в расчетах. В самом простом варианте, когда инвестор планирует разместить деньги на депозите, защитив их от инфляции, в качестве основы для расчета ставки применяют прогнозируемый индекс инфляции. Если кроме сбережения финансов планируется еще и получение дополнительной прибыли, то к ставке инфляции добавляется желаемый процент дохода. При инвестициях, особенно долгосрочных, необходимо учитывать не только инфляцию и норму ожидаемой прибыли, но различные сопутствующие риски. Поэтому в ставку дисконтирования закладываются еще и так называемые премии за риск, а при пользовании заемными средствами для реализации инвестиционного проекта к ставке добавляют еще процент по банковским кредитам, выпуску облигаций и т. п.
Чаще всего при анализе окупаемости дисконтная ставка складывается из безрисковой базовой доходности, приравненной к ключевой ставке ЦБ РФ или средневзвешенному проценту по банковским депозитам с добавлением премии за риск.
Пример
Корпорация должна решить, следует ли вводить новые линейки продуктов. Новый продукт будет иметь расходы на запуск, эксплуатационные расходы, а также входящие денежные потоки в течение шести лет.
Этот проект будет иметь немедленный (T = 0) отток денежных средств в размере $ 100 000 (которые могут включать в себя механизмы, а также расходы на обучение персонала). Другие оттоки денежных средств за 1-6 лет ожидаются в размере $ 5000 в год. Приток денежных средств, как ожидается, составит $ 30 000 за каждый год 1-6. Как только компания получает прибыль от реализации проекта (например, $ 25 000 после первого года), она кладёт их в банк под 10 % годовых на оставшееся до конца проекта время (то есть на оставшиеся 5 лет для первых $ 25 000). Все денежные потоки после уплаты налогов, и на 7 год никаких денежных потоков не планируется. Ставка дисконтирования составляет 10 %.
Таким образом, требуется оценить, какая сумма больше:
- 100000⋅(1+0.1)t≶∑i=1tpi⋅(1+0.1)(t−i){\displaystyle 100\,000\cdot (1+0.1)^{t}\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(t-i)}}, где pi{\displaystyle p_{i}} — доход от проекта, полученный в i-й год реализации проекта, t — общая длительность проекта. Поделим обе части на (1+0.1)t{\displaystyle (1+0.1)^{t}}:
- 100000≶∑i=1tpi⋅(1+0.1)(−i){\displaystyle 100\,000\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(-i)}}.
Каждое слагаемое в правой части неравенства — это приведённая стоимость денег по годам. Например, $ 25 000, полученные от реализации проекта после первого года и положенные в банк на 5 лет, дадут такой же доход, как $ 22 727, положенные в банк в начальный момент времени на 6 лет. Таким образом, приведённая стоимость (PV) может быть рассчитана по каждому году:
| Год | Денежный поток | Приведённая стоимость |
|---|---|---|
| T=0 | −100000(1+0.10){\displaystyle {\frac {-100\,000}{(1+0.10)^{0}}}} | – $ 100 000 |
| T=1 | 30000−5000(1+0.10)1{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{1}}}} | $ 22 727 |
| T=2 | 30000−5000(1+0.10)2{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{2}}}} | $ 20 661 |
| T=3 | 30000−5000(1+0.10)3{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{3}}}} | $ 18 783 |
| T=4 | 30000−5000(1+0.10)4{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{4}}}} | $ 17 075 |
| T=5 | 30000−5000(1+0.10)5{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{5}}}} | $ 15 523 |
| T=6 | 30000−5000(1+0.10)6{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{6}}}} | $ 14 112 |
Сумма всех этих значений является настоящей чистой приведённой стоимостью, которая равна $ 8881.52. Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем класть деньги в банк (под 10 % годовых с капитализацией процентов), и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
Тот же пример с формулами в Excel:
- NPV (ставка, net_inflow) + initial_investment
- PV (ставка, year_number, yearly_net_inflow)
При более реалистичных проблемах необходимо будет рассмотреть другие факторы, как расчет налогов, неравномерный денежный поток и ценности, а также наличие альтернативных возможностей для инвестиций.
Кроме того, если мы будем использовать формулы, упомянутые выше, для расчёта NPV — то мы видим, что входящие потоки (притоки) денежных средств являются непрерывными и имеют такую же сумму; и подставив значения в формулу
- 1−(1+i)−ni{\displaystyle {\frac {1-(1+i)^{-n}}{i}}} мы получим 1−(1+0.1)−60.1=4.3553{\displaystyle {\frac {1-(1+0.1)^{-6}}{0.1}}=4.3553}.
И если умножить полученное значение на денежные потоки (CF), и учесть первоначальные затраты, то в итоге вычислим чистую приведённую стоимость (NPV):
- 4.3553(30000−5000)−100000=$8881.52{\displaystyle -100\,000=\$\,8\,881.52}
Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем ничего не делать, и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
Стоимость денег со временем изменяется
Всем известен тот факт,
что стоимость денег со временем изменяется
и дело здесь даже не столько в инфляции,
сколько в свойстве денег работать и
приносить доход. Всем известна народная
мудрость: Время — деньги. Она означает,
что со временем правильно сделанные
инвестиции способны приносить определённый
доход.
Именно поэтому сегодняшние
10000 рублей стоят не столько, во сколько
они оценивались год назад или во сколько
будут оценены через один год в будущем.
Ведь если вложить эти деньги под
максимально надёжный банковский процент,
то в следующем году сумма в 10000 рублей
превратится уже в 10500 рублей.
При прочих равных
условиях вы всегда предпочтёте получить
деньги сегодня, а не завтра. Ну а если и
согласитесь на определённую отсрочку,
то скорее всего с условием получения
уже несколько большей суммы. Вот например
представьте себе такую ситуацию, когда
ваш работодатель задерживает зарплату
(а это в нашей стране, к сожалению, далеко
не редкость). По справедливости он должен
был бы выплатить вам деньги с процентами
за тот срок на который была задержка,
но это уже из разряда фантастики (опять
таки — к сожалению), тут уж хотя-бы свои
получить, не говоря о какой-либо
компенсации.
Итак, давайте пока остановимся на том, что стоимость денег не является величиной постоянной и, как правило, при прочих равных условиях – с течением времени стоимость денег имеет свойство снижаться. Подробнее об этом читайте здесь: «Что такое временная стоимость денег».
Как пользоваться показателем IRR для оценки эффективности инвестиционного капитала проекта
Любой инвестиционный проект имеет несколько важных условий: первоначальные вложения, определенный срок работы проекта и полученная прибыль за этот период. IRR демонстрирует ставку кредита, при значении которой инвестиция не приведет к убыткам. То есть, тот уровень прибыли в процентах, на котором вложения вернутся и проект окупится, но ничего не принесет дополнительно.
Основное правило оценки проектов для инвестиций выглядит так: если значение IRR рассматриваемого проекта больше суммы капитала, то проект можно открывать. С учетом того, что показатель может считаться или переводиться в проценты, IRR показывает тот процент, при котором заемные средства окупятся. И если полученное значение больше ставки кредита (процента, под который были взяты средства для вложения в проект), то дело принесет прибыль.
Так, к примеру, если взять в банке кредит под 12% годовых и вложить в проект, который даст 17% годовых, то будет прибыль. Если же внутренняя норма доходности проекта будет меньше 12%, проект даст лишь убытки. Сами банки работают по той же схеме: к примеру, привлекают у населения средства под 10% в год и выдают кредиты под 20% в год.
Рассчитав IRR, инвестор получает верхнюю планку допустимой стоимости заемного капитала, который вкладывается. Если цена капитала выше, чем IRR, проект убыточен. Если для компании стоимость капитала ниже найденного IRR проекта, компания сможет существовать за разницу между процентами банковского займа и прибыльностью вложений.
Пример 1: срочный вклад в «Сбербанке»
Данный пример расчета IRR наиболее простой и понятный. Исходные данные такие: в наличии есть 6 000 000 рублей, которые можно положить на депозит в «Сбербанк», сделав вклад на 3 года под 9% в год без капитализации или 10.29% в год с капитализацией каждый месяц.
В нашем примере проценты планируется снимать в конце года, поэтому капитализации не будет и получится 9% в год – сумма получается 6 000 000 х 0.09 = 540 000 дохода в год. По завершении третьего года можно будет снять проценты за него и основную сумму, закрыв депозит.
считается инвестиционным проектом, для него можно рассчитать IRR. IRR для инвестиции в депозит равна процентной ставке депозита – 9%. И если 6 000 000 рублей были накоплены или остались в наследство, их можно вкладывать (ведь стоимость капитала – 0). Если же деньги планируется взять в кредит в банке и вложить в другой, то процентная ставка заемных средств должна быть ниже 9%, если выше – проект не окупится.
Пример 2: покупка квартиры с целью заработка на сдаче ее в аренду
Тут исходные данные такие: объектом инвестирования является квартира, которую планируется сдавать в аренду. Ее покупка будет стоить те же 6 000 000 рублей. Арендная плата будет поступать в размере 30 000 в месяц, за год 360 000 рублей, за 3 – 1 080 000. Получается, что если брать в расчет 3 года, то положить средства в банк выгоднее.
IRR проекта при условии покупки и сдачи в аренду квартиры в течение 3 лет, а потом продажи, равна 6%. То есть, если брать заемные средства на реализацию проекта, процент должен быть меньше 6%, чтобы получать прибыль. И на протяжении 10, 15 лет IRR меняться не будет, исключением является лишь ситуация с подорожанием квартиры.
Внутренняя норма доходности – важный и интересный показатель, который при правильном использовании можно применять достаточно эффективно для просчета прибыльности разных инвестиционных проектов, особенно когда речь идет об их сравнении и выборе наиболее доходного.
Рентабельность производства
Рентабельность производства — это отношение чистой прибыли к стоимости основных фондов и оборотных средств. Фактически рентабельность производства показывает эффективность работы всей компании. Многопрофильные предприятия рассчитывают рентабельность по каждому виду производства отдельно. Также можно вычислить рентабельность производства отдельного вида продукции или рентабельность работы конкретного участка производства, например цеха.
Rпр = П / (Цс Цо) × 100%,
П — прибыль;
Цс — стоимость основных фондов компании;
Цо — стоимость оборотных активов с учетом амортизации и износа.
Практическое применение NPV (чистой текущей стоимости)
Расчёт NPV позволяет оценить целесообразность инвестирования денежных средств. Возможны три варианта значения NPV:
- NPV > 0. Если чистая текущая стоимость имеет положительное значение, то это свидетельствует о полной окупаемости инвестиций, а значение NPV показывает итоговый размер прибыли инвестора. Инвестиции являются целесообразными в следствие их экономической эффективности.
- NPV = 0. Если чистая текущая стоимость имеет нулевое значение, то это свидетельствует об окупаемости инвестиций, но инвестор при этом не получает прибыль. Например, если были использованы заёмные средства, то денежные потоки от инвестиционных вложений позволят в полном объеме рассчитаться с кредитором, в том числе выплатить причитающиеся ему проценты, но финансовое положение инвестора при этом не изменится. Поэтому следует поискать альтернативные варианты вложения денежных средств, которые бы имели положительный экономический эффект.
- NPV
В результате проведённых расчётов проект А следует отклонить, проект Б находится в точке безразличия для инвестора, а вот проекты В и Г следует использовать для вложения средств. При этом, если необходимо выбрать только один проект, то предпочтение следует отдать проекту В, невзирая на то, что сумму недисконтированных денежных потоков за 10 лет он генерирует меньше, чем проект Г.
Пример расчета
Можно на примере рассчитать значение ЧДД.
Допустим по годам денежные вливания были следующего характера:Нулевой год: минусовые вложения -1000,Первый год: показатель +200,Второй год: значение + 300,Третий год: +700.
К примеру, ставка дисконта 12%.
NPV = -1000 / (1+0.12)^0 + 200 / (1+0.12)^1 + 300/(1+0.12)^2 + 700/(1 +0.12)^3 = -1000 + 200* 0,89286 + 300 *0,79719 + 700* 0,71178 = -1000 + 178,57 + 239,16 + 498,25 =
= -84,02 < 0.
Экономический смысл – нужно привести все денежные потоки к настоящему моменту (в этом случае нулевой год) и определить их сумму, при отрицательном результате вложений больше, чем прибыли, такой проект отводится.
Расчет и прогнозирование будущего денежного потока (CF) в Excel
Денежный поток представляет собой количество денежных средств, которым располагает компания/предприятие в данный момент времени. Денежный поток отражает финансовую устойчивость компании. Для расчета денежного потока необходимо из притока денежных (CI, Cash Inflows) средств отнять отток (CO, Cash Outflows), формула расчета будет выглядеть следующим образом:
Определение будущего денежного потока инвестиционного проекта очень важно, поэтому рассмотрим один из методов прогнозирования с помощью программы MS Excel. Статистическое прогнозирование денежных потоков возможно только в том случае если инвестиционный проект уже существует и функционирует
То есть денежные средства необходимы для увеличения его мощности или его масштабирования. Хочется заметить, что если проект венчурный и не имеет статистических данных по объемам производства, продажам, затратам, то для оценки будущего денежного дохода используют экспертный подход. Эксперты соотносят данный проект с аналогами в данной сфере (отрасли) и оценивают потенциал возможного развития и возможных денежных поступлений.
При прогнозировании объемов будущих поступлений необходимо определить характер зависимости между влиянием различных факторов (формирующих денежные поступления) и самого денежного потока. Разберем простой пример прогнозирования будущих денежных поступлений по проекту в зависимости от затрат на рекламу. Если между данными показателями наблюдается прямая взаимосвязь, то можно спрогнозировать какие будут денежные поступления в зависимости от затрат, с помощью линейной регрессии в Excel и функции «ТЕНДЕНЦИЯ». Для этого запишем следующую формулу для затрат на рекламу в 50 руб.
Денежный поток (CF). В12=ТЕНДЕНЦИЯ(B4:B11;C4:C11;C12)
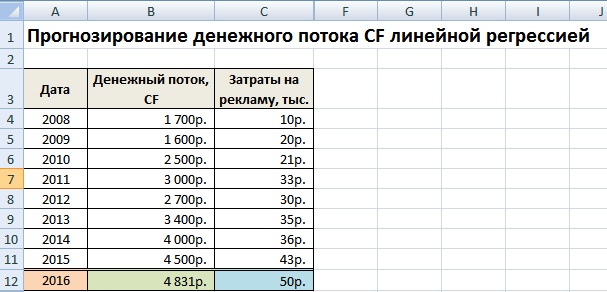
Размер будущего денежного потока будет составлять 4831 руб. при затратах на рекламу в 50 руб. В реальности на определение размера будущих поступлений влияет намного большее количество факторов, которые следует отбирать по степени влияния и их взаимосвязи между собой с помощью корреляционного анализа.
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Необходимость расчёта
 Вычисление чистой приведенной стоимости – один из наиболее популярных методов прогнозирования эффективности инвестиционных программ. Оценка значения данного показателя позволяет дать ответ на главный для предпринимателя вопрос: «Вкладывать денежные средства в проект или нет?».
Вычисление чистой приведенной стоимости – один из наиболее популярных методов прогнозирования эффективности инвестиционных программ. Оценка значения данного показателя позволяет дать ответ на главный для предпринимателя вопрос: «Вкладывать денежные средства в проект или нет?».
Необходимость определения NPV вызвана тем, что коэффициент позволяет не только оценить величину прогнозируемой прибыли, но и учесть тот факт, что любая сумма денежных средств в текущий момент времени обладает большей реальной стоимостью, чем такая же сумма в будущем.
Так, например, вместо инвестирования проекта предприниматель может:
- Открыть депозитный счёт в банке и получать ежегодно прибыль в соответствии с процентной ставкой.
- Приобрести имущество, ценность которого в будущем возрастёт на величину инфляции.
- Спрятать денежные средства.
Поэтому вычисление показателя происходит с использованием заданной процентной ставки дисконта, которая позволяет учесть факторы инфляции и риска, а также оценить эффективность проекта по сравнению с альтернативными вариантами вложения средств.
Достоинства и недостатки доходного подхода к оценке бизнеса рассмотрены здесь.
Что такое чистый дисконтированный доход (ЧДД)
При оценке инвестиционной привлекательности отдельных финансовых инструментов или целых проектов применяется показатель именуемый чистым дисконтированным доходом. При его упоминании часто используют аббревитуру ЧДД, а в английской транскрипции его называют Net Present Value (NPV).
Говоря простыми
словами, ЧДД представляет собой итог
всех денежных поступлений в рассматриваемый
инвестиционный проект и оттоков из
него. Эта величина наглядно показывает
инвестору есть ли перспективы у
конкретного инвестпроекта (в плане
получения прибыли) и стоит ли в него
вкладываться.
Дисконтирование
в данном случае позволяет привести все
денежные потоки к одному моменту времени.
Анализ
инвестиционного проекта при расчёте
ЧДД включает в себя несколько основных
этапов:
- Оценка входящих
и исходящих денежных потоков в плане
результативности (эффективности). А
именно – с точки зрения тех результатов,
к которым приводят очередные вложения; - Определение
ставки дисконтирования; - Дисконтировать
все денежные потоки согласно установленной
ставке; - Суммировать
продисконтированные денежные потоки
и получить в итоге величину ЧДД.
Существует три основных
значения ЧДД:
- Положительное
(ЧДД>0); - Отрицательное
(ЧДД<0); - Нейтральное
(ЧДД=0).
ЧДД>0 говорит о том, что положительные денежные потоки превалируют над отрицательными и свидетельствует об инвестиционной привлекательности рассматриваемого проекта;
ЧДД<0, напротив, говорит о том, что отток капитала превышает величину поступлений денежных средств и предупреждает инвестора о потенциальной убыточности рассматриваемого проекта;
ЧДД=0 показывает инвестору относительную нейтральность анализируемого проекта. Он не приносит ни прибыли, ни убытка. Вкладываться в такой проект стоит лишь при наличии другой заинтересованности (помимо получения прибыли), например если дело касается спонсорской поддержки или каких-либо социально значимых проектов.
Определение
ставки дисконтирования
Определение
максимально достоверной ставки
дисконтирования — процесс довольно
сложный, требующий объективного
кропотливого анализа множества
составляющих рассматриваемого проекта.
В самом общем
случае при этом необходимо учитывать
следующие показатели:
- Уровень
инфляции (текущий и в динамике); - Проценты
получаемые по вкладам; - Средний
процент доходности получаемой от ценных
бумаг; - Прогнозируемые
аналитиками данные по будущей доходности; - Общая стоимость
всех вложений в проект и уровень
вовлечённости в него других инвесторов.
Формула и пример
расчёта ЧДД
Для расчёта
величины чистого дисконтированного
дохода используют следующую формулу:
Чтобы не быть
голословным, я приведу простой пример
расчёта величины ЧДД исходя из данных
гипотетического инвестиционного проекта
величина денежных потоков по которому
приведена в нижеследующей таблице.
| Год (порядковый номер) |
Величина денежного потока, млн рублей |
| 100 | |
| 1 | -150 |
| 2 | 200 |
| 3 | 300 |
Предположим,
что значение ставки дисконтирования в
данном случае равно 10%. Тогда расчёт
будет выглядеть следующим образом:
100/(1+0,1)^0
+ (-150)/(1+0,1)^1 + 200/(1+0,1)^2 + 300/(1+0,1)^3 = 322,11
Полученное
положительное значение ЧДД говорит о
способности рассматриваемого проекта
генерировать прибыль. В приведённом
примере всё просто и понятно, ведь он
не включает в себя весь спектр
предварительных работ и расчётов –
ставка дисконтирования уже рассчитана
и величины денежных потоков определены.
Это теория, а в реальности всё конечно
сложнее.
Надо понимать,
что при расчётах реальных инвестпроектов
следует использовать только достоверную,
тщательно выверенную информацию.
Расчет чистого дисконтированного дохода
Показатель чистого дисконтированного дохода (ЧДД) по-английски называется Net present value, поэтому общепринято сокращенно его называть NPV. Существует ещё альтернативное его наименование – Чистая приведенная стоимость.
NPV определяет сумму приведенных к нынешнему дню дисконтированных значений платежей, которые являются разностью между притоками и оттоками. Если говорить простым языком, то данный показатель определяет, какую сумму прибыли планирует получить инвестор за вычетом всех оттоков после того, как окупится первоначальный вклад.
В программе Excel имеется функция, которая специально предназначена для вычисления NPV. Она относится к финансовой категории операторов и называется ЧПС. Синтаксис у этой функции следующий:
Аргумент «Ставка» представляет собой установленную величину ставки дисконтирования на один период.
Аргумент «Значение» указывает величину выплат или поступлений. В первом случае он имеет отрицательный знак, а во втором – положительный. Данного вида аргументов в функции может быть от 1 до 254. Они могут выступать, как в виде чисел, так и представлять собой ссылки на ячейки, в которых эти числа содержатся, впрочем, как и аргумент «Ставка».
Проблема состоит в том, что функция хотя и называется ЧПС, но расчет NPV она проводит не совсем корректно. Связано это с тем, что она не учитывает первоначальную инвестицию, которая по правилам относится не к текущему, а к нулевому периоду. Поэтому в Экселе формулу вычисления NPV правильнее было бы записать так:
Естественно, первоначальная инвестиция, как и любой вид вложения, будет со знаком «-».
Пример вычисления NPV
Давайте рассмотрим применение данной функции для определения величины NPV на конкретном примере.
- Выделяем ячейку, в которой будет выведен результат расчета NPV. Кликаем по значку «Вставить функцию», размещенному около строки формул.
Запускается окошко Мастера функций. Переходим в категорию «Финансовые» или «Полный алфавитный перечень». Выбираем в нем запись «ЧПС» и жмем на кнопку «OK».
После этого будет открыто окно аргументов данного оператора. Оно имеет число полей равное количеству аргументов функции. Обязательными для заполнения является поле «Ставка» и хотя бы одно из полей «Значение».
В поле «Ставка» нужно указать текущую ставку дисконтирования. Её величину можно вбить вручную, но в нашем случае её значение размещается в ячейке на листе, поэтому указываем адрес этой ячейки.
В поле «Значение1» нужно указать координаты диапазона, содержащего фактические и предполагаемые в будущем денежные потоки, исключая первоначальный платеж. Это тоже можно сделать вручную, но гораздо проще установить курсор в соответствующее поле и с зажатой левой кнопкой мыши выделить соответствующий диапазон на листе.
Так как в нашем случае денежные потоки размещены на листе цельным массивом, то вносить данные в остальные поля не нужно. Просто жмем на кнопку «OK».
Расчет функции отобразился в ячейке, которую мы выделили в первом пункте инструкции. Но, как мы помним, у нас неучтенной осталась первоначальная инвестиция. Для того, чтобы завершить расчет NPV, выделяем ячейку, содержащую функцию ЧПС. В строке формул появляется её значение.
После символа «=» дописываем сумму первоначального платежа со знаком «-», а после неё ставим знак «+», который должен находиться перед оператором ЧПС.
Можно также вместо числа указать адрес ячейки на листе, в которой содержится первоначальный взнос.
Для того чтобы совершить расчет и вывести результат в ячейку, жмем на кнопку Enter.
Результат выведен и в нашем случае чистый дисконтированный доход равен 41160,77 рублей. Именно эту сумму инвестор после вычета всех вложений, а также с учетом дисконтной ставки, может рассчитывать получить в виде прибыли. Теперь, зная данный показатель, он может решать, стоит ему вкладывать деньги в проект или нет.
Урок: Финансовые функции в Excel
Как видим, при наличии всех входящих данных, выполнить расчет NPV при помощи инструментов Эксель довольно просто. Единственное неудобство составляет то, что функция, предназначенная для решения данной задачи, не учитывает первоначальный платеж. Но и эту проблему решить несложно, просто подставив соответствующее значение в итоговый расчет.
Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.