Дисконтирование в расчетах для целей мсфо

Задача обратная наращению (начислению процентов)

В финансовых расчетах часто приходится решать задачу обратную наращению (задачу дисконтирования): по известной наращенной сумме найти начальную сумму. Например, какую сумму положить на депозит, чтобы через 5 лет получить 500 тыс. руб.

Введем обозначения:PV — present value, современная величина, первоначальной сумма.FV — future value, будущая величина, наращенная сумма.I = (FV — PV) — interest money, процентные деньги, проценты. Представляют собой сумму дохода.

Оценка доходности финансовых операций по величине процентных денег I редко используется, т.к. зависит от первоначальной суммы PV и срока наращения. Более удобным показателем является процентная ставка, характеризующая скорость наращения.

r = I/PV = (FV-PV)/PV — interest, процентная ставка.

Обычно процентная ставка известна из условий финансовой операции (например, из условий депозитного или кредитного договора), тогда для наращенной суммы можно записать:

FV = PV*(1+r).

Таким образом, зная процентную ставку и начальную сумму, мы определяем наращенную сумму.

• Формулы расчета процентов
• Формулы расчета сложных процентов и выбор вклада

При решении задач дисконтирования надо решить обратную задачу: зная наращенную сумму, определить начальную сумму, или сумму в другой предшествующий момент. Для этого по аналогии с процентной ставкой определим ставку дисконтирования (учетную ставку):

d = I/FV = (FV-PV)/FV — discount rate, ставка дисконтирования, учетная ставка.

Зная ставку дисконтирования и наращенную сумму, решаем задачу дисконтирования (определяем начальную сумму):

PV = FV*(1-d).

Ставка дисконтирования и процентная ставка связаны соотношениями:

r = d * (FV/PV)
d = r * (PV/FV)

Кроме того, т.к. процентная ставка определяется по отношению к начальной сумме, а ставка дисконтирования — к наращенной, процентная ставка больше ставки дисконтирования.

Формула расчета

Дисконтирование будет обратным итогом от инвестирования. К примеру, при инвестировании 100 тыс. рублей по 10% годовых результат равен 110 тыс. рублей: 100 000* (100% + 10%)/100%.

При определении дохода за пару лет прибегают к возведению в степень. Распространенная ошибка – умножение на общую сумму процентов для учета «процентов на проценты». Подобные расчеты допустимы при отсутствии капитализации процентов.

Для определения ставки дисконтирования, необходимо найти начальную сумму инвестирования: конечную прибыль умножить на 100%, а потом разделить на сумму 100%, увеличенных на ставку. Если вложения проходят несколько циклов, то полученную цифру умножают на их число.

В международном формате используют англоязычные термин Future value и present value. В описанном примере FV – 2500 у.е., PV – 1552 у.е. Общая форма дисконтирования:

PV = FV*1/(1+R)^n

1/(1+R)^n – фактор дисконтирования;

R – процентная ставка;

n – количество циклов.

Вычисления достаточно просты, их могут выполнять не только банкиры. Но расчеты можно игнорировать, если понимать суть процесса.

Дисконтирование – изменение денежного потока с будущего до настоящего, т.е. путь финансов идет от суммы, которую требуется получить на определенный момент, к сумме, которая будет инвестирована.

Деньги + время

Рассмотрим еще одну распространенную ситуацию: имеются свободные средства, которые решено положить в банк под проценты. Сумма – 2000 у.е., процентная ставка – 10%. Через год в распоряжении вкладчика уже будет 2200 у.е., т. к. проценты по вкладу составят 200 у.е.

Если привести все это к общей формуле, то выйдет:

2000*(100%+10%)/100% = 2000*1,1 = 2200 у.е.

Если положить 2000 у.е. на 2 года, то итоговая сумма составит 2420 у.е.:

1 год 2000*1,1 = 2200 у.е.

2 год 2200*1,1 = 2420 у.е.

Происходит наращивание без дополнительных взносов. Если срок инвестирования будет продлен, то доход увеличится еще больше. За каждый ход хранения средств на депозите общую сумму вклада за предыдущий год умножают на (1+R) или первоначальный размер инвестиций умножают на (1+R)^n.

Кумулятивный метод

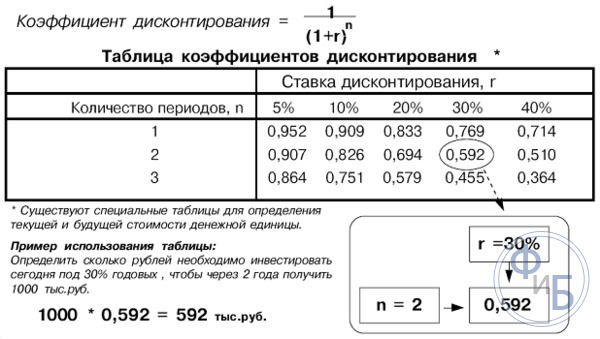
Для упрощения расчетов используют таблицу коэффициентов. При ее применении уже не требуется несколько раз рассчитывать по формуле сумму инвестирования и доходность. Достаточно итоговую прибыль умножить на коэффициент из таблицы, чтобы получить желаемую инвестицию.

Формула для определения коэффициента дисконтирования:

К = 1/(1+Пр)^В,

где В – количество циклов;

Пр – процентная ставка на цикл.

Например, для двухгодичных инвестиций под 20% коэффициент равен:

1*/(1+0,2)^2 = 0,694

Таблицы дисконтирования схожи с таблицами Брадиса, которые помогают школьникам определять корни, косинусы и синусы.

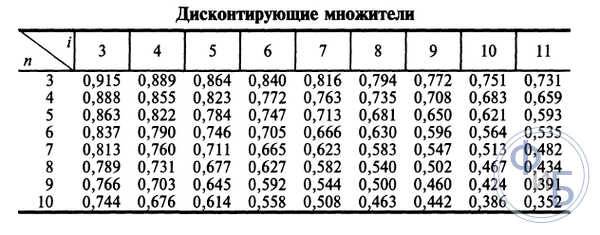
Пользоваться таблицей просто: если известна ставка и число периодов, на пересечении необходимых столбца и строки находят нужный коэффициент.

Усложненные расчеты

В экономике используют несколько усложненный расчет, который учитывает ряд рисков. В формулах используют следующие понятия:

• Безрисковая, ожидаемая и рыночная доходность. Используются в формуле Шарпа для определения экономических рисков.
• Откорректированная модель Шарпа. Определяет влияние рыночных факторов: изменение стоимости ресурсов, политику государства, ценовые колебания.
• Объем капиталовложений, особенности отрасли. Данные используют в более точной версии Френча и Фамы.
• Изменения стоимости актива используется в формуле Кархарта.
• Дивидендные платежи и эмиссия акций. Подобные расчеты принадлежат Гордону. Его метод позволяет точно изучить фондовый рынок и анализировать стоимость акционерных обществ.
• Средневзвешенная цена. Применяют перед определением ставки дисконтирования в кумулятивном методе и учете заемных средств.
• Рентабельность собственности. Применяют для анализа финансовой деятельности компании, активы которой не выставлены на фондовый рынок.
• Субъективный фактор. Используется при мультифакторном анализе деятельности организации сторонними экспертами.
• Рыночные риски. Учитывают при определении ставки дисконтирования на основе отношения рискового к безрисковому инвестированию.

В 1997 году правительство РФ опубликовало собственную методику вычисления рисковой ставки дисконтирования. Эксперты того времени оценили риски в размере 47%. Этот показатель не применяют в обычных формулах, но он является обязательным при расчете инвестиций в зарубежные проекты.

Различные методики расчета позволяют оценить потенциальные инвестиции и построить план размещения финансовых средств. При анализе хоздеятельности компаний на рынке теоретические расчеты дадут ожидаемый эффект, если будут учтены местные реалии. Простые расчеты помогут предсказать доходность, но она будет сильно подвержена колебаниям. Для прогнозирования нужно использовать сложные формулы, которые учитывают большинство рисков на финансовом и фондовом рынке. Более точные данные будут получены только при внутреннем анализе компании.

Формула дисконтирования

Часто возникает обратная задача: предпологается, что через n лет будет получена сумма S_n, надо найти равноценную ей сумму на текущий момент. Это типичная задача при разработке бизнес-планов, расчете окупаемости инвестиций, оценке стоимости бизнеса по величине ожидаемых доходов (доходный подход к оценке стоимости бизнеса). Иными словами, известна сумма S_n, надо определить S. В этом случае путем простых преобразований получаем формулу расчета:

S = S_n/(1+P)n   — Формула дисконтирования

Эта операция называется дисконтированием, она является обратной к вычислению сложных процентов. Часто используется термин «приведение к текущей стоимости». Процентная ставка в этом случае называется ставкой дисконтирования.

Понятие

«Дисконт» можно перевести как уступка за предварительную оплату. Дословно оно означает приведение экономического показателя за определенный временной промежуток к заданному отрезку. При отсутствии экономического образования в подобной терминологии легко запутаться. Но рачительному хозяину стоит разобраться в вопросе, так как большинство люди не подозревают своего участия в «дисконтировании». К примеру, купец обещает продать товар по указанной стоимости через год, когда придет корабль с товаром.

Однако он нуждается в финансовых средствах для приобретения товара, который будет участвовать в меновой операции. Существует два способа получить деньги: обратиться к банкиру за получением кредита или взять средства у будущих покупателей. Купец должен простым языком объяснить последним о ставке дисконтирования. Если клиенты поймут, то успех мероприятия будет обеспечен.

Ставка дисконтирование используется в следующих целях:

• Расчет доходности бизнеса. Инвестор должен знать размер прибыли в будущем, чтобы вложить финансовые средства с желаемой отдачей.
• Оценка деятельности организации. Имеющаяся прибыль не гарантирует хорошую рентабельность.
• Планирование доходности. Выбранный вариант инвестирования должен иметь максимальную отдачу в сравнении с альтернативными вариантами. Например, один бизнес будет иметь определенную прибыль через 1 год, а другой принесет больше средств, но только через два года. Следует сравнить оба предложения по одному знаменателю. Для ясности рассмотрим пример из практики. К потенциальному инвестору обратилось два бизнесмена. Они просят вложить в их дело 2 млн. Первый обещает вернуть 3 млн. через два года, второй – 5 млн. через 6 лет. Как же рассчитать ставку дисконтирования при привлечении заемного капитала?

Коэффициент дисконтирования

Дисконтирование денежного потока за n-й период выполняется путем умножения потока на коэффициент дисконтирования K_n:

K_n= 1/(1+D)n, где

n — Номер периода (шага) дисконтирования
K_n — Коэффициент дисконтирования на шаге n
D — Ставка дисконтирования.

Ставка дисконтирования отражает скорость изменения стоимости денег со временем, чем больше ставка дисконтирования, тем больше скорость.

Коэффициент K_n уменьшается с ростом n, это отражает тот факт, что чем дальше в будущее отстоит от нас ожидаемый денежный поток, тем меньше его стоимость приведенная к текущему значению.

Расчет ставки дисконтирования по методу WACC — средневзвешенной стоимости капитала

Дисконтирование в обычной жизни

Каждый россиянин хотя бы раз задумывался о «стоимости денег». Она особо ощутимо во время покупок в супермаркетах, когда с продуктовой корзины приходится убирать «ненужный» товар. В настоящее время необходимо быть экономным и расчетливым. Под дисконтированием часто понимают экономический показатель, показывающий покупательскую способность денег, стоимость через определенный промежуток времени. Дисконтирование используют для прогнозирования прибыли для инвестиционных проектов. О будущих результатах можно говорить в начале проекта или во время его осуществления при умножении на коэффициент дисконтирования. Но подобное понятие применимо не только к инвестициям, но и в обычной жизни. Например, родители желают оплатить ребенку образование в престижном заведении. Но не у всех есть возможность внести плату в момент поступления. Тогда начинают думать о «заначке», которая предназначена для часа икс. Через 5 лет запланировано поступление ребенка в европейский университет. Стоимость подготовительных курсов 2500 у.е. Выделить подобную сумму из бюджета семьи без ущерба интересов других членов для многих нереально. Выход – заранее открыть вклад в финансовом учреждении. Но как определить сумму вклада, чтобы через пять лет получить 2500 у.е.? Ставка по вкладу 10%. Расчет первоначальной суммы: 2500/(1+0,1)^5 = 1552 у.е. Это и называют дисконтированием.

Простыми словами, если требуется узнать будущую стоимость определенной суммы, то следует «продисконтировать» ее по банковской ставке, которую называют ставкой дисконтирования. В приведенном примере она равна 10%, 2500 у.е. – денежный поток (сумма платежа) через 5 лет, 1552 у.е. – дисконтированная стоимость денежного потока.

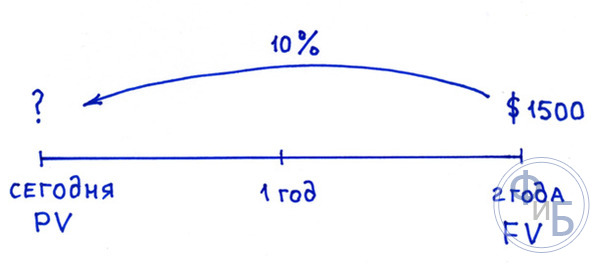
Пример

Пусть мы имеем 100 руб. и кладем их на депозит под 5% годовых с ежегодным начислением процентов и зачислением их во вклад. Тогда через год у нас будет 105 рублей.

S₁ = 100 + 100 × 0.05 = (1+0.05) × 100 = 105

Через два года у нас будет 110.25 рублей.

S₂ = (1+0.05)×(1+0.05) × 100 = (1+0.05)2 × 100 = 110.25

Через три года у нас будет 115.7625 рублей.

S₃ = (1+0.05)3 × 100 = 115.7625

Через n лет у нас будет

S_n = (1+0.05)n × 100

S_n = (1+P)n S, где

Sn — сумма через n периодов начисления процентов
P — процентная ставка за период
S — начальная сумма.

Это формула расчета сложных процентов.

Таким образом, если мы можем положить деньги на депозит с условиями описанными выше, то 100 руб., которые мы получим сейчас, с экономической точки зрения равноценны 105  руб. которые мы получим через год, равноценны 110.25 руб. полученным через два года, равноценны 115.7625 руб. полученным через три года и так далее.

В общем виде: сумма S, полученная сейчас, равноценна сумме (1+P)n S, полученной через n лет.

Практическое использование

При повышении ставки дисконтирования увеличивается срок окупаемости инвестиций. Решение о вложении средств должно приниматься тогда, когда расчеты показывают желаемый срок окупаемости и соответствуют плану капитального инвестирования.

Приведенные формулы не учитывают рыночные риски. Их можно использовать только для теоретического расчета. Для приближения расчета к реальности прибегают к графическому анализу. На графиках представляют данные по движению финансов в определенном интервале времени.

Дисконтирование и наращивание

С помощью простой формулы определяют размер вклада в желаемой временной точке. Расчет стоимости денег в будущем называют «наращиванием». Суть этого процесса легко понять по выражению «время-деньги» — со временем размер вклада увеличивается на размер приращения ежегодными процентами. Вся банковская система основана на этом принципе.

Дисконтирование и наращивание помогают анализировать возможность изменения стоимости средств.

Инвестиционные проекты

Дисконтирование финансовых средств соответствует инвестиционным мотивам бизнеса. То есть инвестор вкладывает средства и получает не человеческие (квалифицированные специалисты, команда) или технические ресурсы (оборудование, склады), а поток денег в будущем. Продолжением этой мысли будет «продуктом любого бизнеса являются деньги». Метод дисконтирования является единственным из существующих, ориентация которого направлена на развитие в будущем, что позволяет инвестиционному проекту развиваться.

Пример выбора инвестиционного проекта. Владельцу денежных средств (600 руб.) предложено вложить их в реализацию проектов «А» и «В». Первый вариант дает доход на протяжении трех лет 400 рублей. Проект «Б» после первых двух лет реализации позволит получить по 200 рублей, а после третьего – 10000 рублей. Инвестор определил ставку 25%. Определим текущую стоимость обоих проектов:

проект «А» (400/(1+0,25)^1+400/(1+0,25)^2+400/(1+0,25)^3)-600 = (320+256+204)-600 = 180 рублей

проект «В» (200/(1+0,25)^1+200/(1+0,25)^2+1000/(1+0,25)^3)-600 = (160+128+512)-600 = 200 рублей

Таким образом, инвестор должен выбрать второй проект. Однако при повышении ставки до 31% оба варианта окажутся равнозначными.

Приведенная стоимость

Дисконтированной стоимостью называют сегодняшнюю стоимость будущего денежного потока или будущий платеж без «скидки» за предварительную оплату. Ее часто называют приведенной стоимостью – будущий денежный поток, соотнесенный к сегодняшнему дню. Однако это не совсем одинаковые понятия. Привести к текущему времени можно не только одну будущую стоимость, но и настоящею стоимость к нужному времени в будущем. Приведенная стоимость более обширно, чем дисконтированная стоимость. В английском языке понятие приведенная стоимость отсутствует.

Расчет окупаемости инвестиций

Ставка дисконтирования используется при расчете срока окупаемости и оценке экономической эффективности инвестиций для дисконтирования денежных потоков, иными словами, для перерасчета стоимости потоков будущих доходов и расходов в стоимость на настоящий момент.

В этом случае в качестве ставки дисконтирования принимается один из вариантов:

• Доходность альтернативного проекта.
• Стоимость доступного кредита.
• WACC — cредневзвешенная стоимость капитала.
• Экспертная оценка.
• Желаемая доходность инвестиционного проекта.
• Кумулятивный метод, базирующийся на оценке рисков проекта.

Особую роль при расчете инвестиционнго проекта имеет IRR (внутренняя норма доходности) — значение ставки дисконтирования при которой NPV проекта равно 0.

Способы расчета

Применяются два способа расчета NCF – прямой и косвенный. Прямой используется при составлении отчета о движении ДС и характеризует состояние оборотных средств на расчетных счетах компании. Иными словами, прямой способ напоминает расчет прибыли кассовым методом. Чтобы было более понятно, поясню: при планировании личных финансов используется именно прямой метод – вы считаете, сколько денег получили и сколько израсходовали. Остаток и будет равен вашему личному NCF. Эти деньги вы можете включить в расходы следующего месяца, отложить «на черный день» или инвестировать. В случае если вы не намерены тратить эти средства, они будут именоваться свободным денежным потоком.

Косвенный метод соотносится с современными стандартами финансовой отчетности и позволяет получить более детальную информацию об объеме свободных денежных средств и структуре статей их движения. При косвенном методе NCF рассчитывается исходя из чистой прибыли, откорректированной на некоторые величины. Мы знаем, что чистая прибыль – это показатель в стоимостном выражении, представляющий собой остаток средств после исполнения всех обязательств. Эта сумма распределяется на усмотрение собственников компании: можно направить ее на увеличение собственного капитала, а можно потратить на что-то полезное или выплатить доходы лицам, имеющим доли в уставном капитале.

Далее разберем каждый способ более подробно.

Прямой метод расчета ЧДП

Чтобы найти чистый денежный поток путем применения прямого метода, достаточно использовать регистры бухгалтерского учета:

• кассовая книга;
• выписки банка;
• оборотно-сальдовые ведомости и анализы счетов учета денежных средств в разрезе статей движения.

Таким образом, формула расчета NCF прямым методом выглядит так:

\

Поп – поступления от покупателей;

​\( АвП \)​ – авансы полученные;

​\( ПП \)​ – прочие поступления (сюда входят кредиты и займы);

​\( ОП \)​ – оплаты поставщикам за материалы, товары, услуги;

​\( АвВ \)​ – выданные авансы;

​\( ЗП \)​ – выплаченная заработная плата;

​\( НС \)​ – налоги и сборы;

​\( ПВ \)​ – прочие выплаты (погашения займов и процентов, комиссии банков, прочие расходы).

Косвенный метод расчета ЧДП

И снова мы возвращаемся к вопросу, почему иногда бывает так, что прибыль есть, а денег нет. Для ответа на этот вопрос и существует косвенный метод расчета ЧДП.

Прежде всего, следует разобраться: в чем разница между свободным денежным потоком и чистой прибылью.

Свободный денежный поток – это остаток денег на счете на конец периода после исполнения всех обязательств. Предположим, на последнее число месяца мы погасили задолженность поставщикам в соответствии с графиком, выплатили заработную плату, внесли платежи по долговым обязательствам и проценты, уплатили налоги. Осталась некая сумма, которую можно потратить на усмотрение собственника. Например, приобрести ценные бумаги.

Чистая прибыль не измеряется живыми деньгами. Эта величина складывается с учетом различных составляющих, некоторые из которых не подлежат оплате.

Пример – те же самые амортизационные отчисления. В расчете чистой прибыли они участвуют, но расходовать денежные средства на них не нужно.

Другой пример: резервы по сомнительным долгам. Задолженность покупателя, признанная сомнительной, переносится в резерв и частично уменьшает сумму налогооблагаемой, а затем и чистой прибыли.

Можно привести еще много примеров хозяйственных операций, в которых живые деньги не требуются, однако эти операции влияют на финансовый результат.

Кроме того, в формировании чистой прибыли не участвуют заемные средства. Только уплаченные по ним проценты можно отнести на издержки.

Чистый денежный поток косвенным методом определяется так:

\

​\( Δ \)​ – изменение (прирост) соответствующего показателя;

​\( ДЗ \)​ – дебиторка;

​\( ТМЦ \)​ – запасы материалов, товаров, сырья, полуфабрикатов;

​\( КЗ \)​ – кредиторка;

​\( ФВ \)​ – финансовые вложения;

​\( АВ \)​ – выданные авансы;

​\( АП \)​ – полученные авансы;

​\( ДБП, РБП \)​ – доходы и расходы будущих периодов;

​\( РФ \)​ – резервный фонд.

Все эти показатели можно взять из финансовой отчетности.

Чуть ниже мы рассчитаем сумму чистого денежного потока прямым и косвенным методом в редакторе Excel.