Факторный анализ предприятия. этапы проведения. методы

Структурное моделирование уравнение

Программное обеспечение для моделирования структурных уравнений обычно используется для выполнения подтверждающего факторного анализа. LISREL , EQS, AMOS, Mplus и пакет lavaan в R — популярные программы. CFA также часто используется в качестве первого шага для оценки предлагаемой модели измерения в модели структурного уравнения. Многие правила интерпретации, касающиеся оценки соответствия модели и модификации модели при моделировании структурными уравнениями, в равной степени применимы к CFA. CFA отличается от моделирования структурным уравнением тем, что в CFA нет направленных стрелок между скрытыми факторами . Другими словами, в то время как в CFA не предполагается, что факторы напрямую вызывают друг друга, SEM часто определяет конкретные факторы и переменные как причинные по своей природе. В контексте SEM CFA часто называют «моделью измерения», а отношения между скрытыми переменными (с направленными стрелками) называют «структурной моделью».

Мастер настройки

• Критерий значимости факторов:
  • По собственному значению — отбираются только факторы с собственными значениями равными или большими 1. Считается, что те факторы, у которых этот показатель меньше 1, не вносят значительного вклада в объяснение результата.
  • По дисперсии — факторы отбираются по доле объясняемой дисперсии. В этом случае выбирают столько факторов, чтобы в сумме они объясняли не менее 70-75% дисперсии. В отдельных вариантах порог дисперсии может достигать 85-90%.
  • Задать число факторов — количество значимых факторов выбирается аналитиком самостоятельно.

Значение каждого критерия можно задать в специальном поле справа от соответствующей ему радиокнопки.

• Метод получения окончательного решения
  • Без вращения — исходные факторы, полученные методом главных компонент, остаются без изменений.
  • Варимакс — критерием является упрощение описания каждого фактора. В результате максимизируется нагрузка на каждый фактор относительно небольшого числа переменных, а факторные нагрузки остальных переменных минимизируются. Рекомендуется выбирать, когда требуется обеспечить высокую интерпретируемость результатов факторного анализа.
  • Квартимакс — данный критерий упрощает описание каждой переменной, то есть уменьшает число факторов, связанных с этой переменной.
• Ограничить число выходных факторов — необязательный флаг, при активации которого можно задать ограничивающее число выходных факторов в соответствующем поле области.

Общая характеристика метода цепных подстановок

Одним из универсальных и распространенных элементов экономического анализа является метод цепных подстановок. Используют его для определения степени воздействия отдельных факторов на конкретные совокупные показатели. Он позволяет:

Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс

• объяснить, как конкретный фактор на них отражается, влияет на их изменение;
• путем расчета выяснить отклонения одних типов значений от других (фактических от нормативных).  

Для него характерна универсальность и сравнительная простота в расчетах

Это позволяет применять его часто и, что немаловажно, при анализе разных факторных моделей (FACTOR MODEL). Мультипликативных, кратных и т

д. 

Суть метода подстановки состоит в последовательной замене значений факторов:

• базисных на отчетные;
• либо плановых на фактические.

Изначально взаимосвязанные факторы размещают определенным порядком. Сначала – количественные, те, которые выражают количество, подлежат учету. Вслед за ними – качественные, характеризуемые признаками, внутренними качествами. 

Наглядный пример. Предположим, нужно выяснить влияние количества работников и производительности (результативности) труда на объем производимых хозяйственных товаров. С этой целью сначала определяют влияние количественного фактора (численности персонала), а только потом – качественного (продуктивности, производительности).

Когда качественных и количественных факторов много, руководствуются принципом «сначала наиболее общие, а затем остальные». Т. е. факторы первого порядка (определяют результат), второго порядка (воздействуют на результат) и т. д. Затем с их участием при помощи расчетов, заменяя значения, вычитая, определяют влияние факторов на изменение анализируемого совокупного показателя.

Оценка стоимости бизнеса	Финансовый анализ по МСФО	Финансовый анализ по РСБУ
Расчет NPV, IRR в Excel	Оценка акций и облигаций

Факторный анализ рентабельности

ФА рентабельности проводится для анализа рациональности распределения ресурсов. В результате можно определить, какие факторы наибольшим образом влияют на конечный результат. В результате можно оставить только те факторы, которые наилучшим образом воздействуют на эффективность. На основании полученных данных можно изменить ценовую политику компании. На себестоимость продукции могут влиять следующие факторы:

• постоянные издержки;
• переменные издержки;
• прибыль.

Уменьшение издержек провоцирует повышение прибыли. При этом себестоимость не изменяется. Можно сделать вывод о том, что на прибыльность влияют имеющиеся издержки, а также объем проданной продукции. Факторный анализ позволяет определить степень влияния этих параметров. Когда имеет смысл его проводить? Основной повод к проведению – уменьшение или повышение прибыльности.

Факторный анализ проводится посредством следующей формулы:

Rв= ((Вт-СБ -КРБ-УРБ)/ Вт) — (ВБ-СБ-КРБ-УРБ)/ВБ, где:

ВТ – выручка за нынешний период;

СБ – себестоимость за нынешний период;

КРБ – коммерческие траты за нынешний период;

УРБ – управленческие траты за предшествующий период;

ВБ – выручка за предшествующий период;

КРБ – коммерческие траты за предшествующий период.

Иные формулы

Рассмотрим формулу расчета степени воздействия себестоимости на прибыльность:

Rс= ((Вт-СБот -КРБ-УРБ)/ Вт) — (Вт-СБ-КРБ-УРБ)/Вт,

СБот – это себестоимость продукции за нынешний период.

Формула для расчета влияния управленческих трат:

Rур= ((Вт-СБ -КРБ-УРот)/ Вт) — (Вт-СБ-КРБ-УРБ)/Вт,

УРот – это управленческие траты.

Формула для вычисления степени воздействия коммерческих издержек:

Rк= ((Вт-СБ -КРо-УРБ)/ Вт) — (Вт-СБ-КРБ-УРБ)/Вт,

КРо – это коммерческие траты за предыдущее время.

Совокупное воздействие всех факторов высчитывается по следующей формуле:

Rоб=Rв+Rс+Rур+Rк.

ВАЖНО! При расчетах имеет смысл высчитывать влияние каждого фактора в отдельности. Результаты общего ФА имеют небольшую ценность

Пример

Рассмотрим показатели организации за два месяца (за два периода, в рублях). В июле доход организации составил 10 тысяч, себестоимость продукции – 5 тысяч, административные траты – 2 тысячи, коммерческие траты – 1 тысяча. В августе доход компании составил 12 тысяч, себестоимость продукции – 5,5 тысяч, административные траты – 1,5 тысячи, коммерческие траты – 1 тысяча. Проводятся следующие расчеты:

R=((12 тысяч-5,5 тысяч-1 тысяча-2 тысячи)/12 тысяч)-((10 тысяч- 5,5 тысяч-1 тысяча-2 тысячи)/10 тысяч)=0,29-0,15=0,14

Из этих расчетов можно сделать вывод о том, что прибыль организации повысилась на 14%.

ИНТЕГРАЛЬНЫЙ МЕТОД В АНАЛИЗЕ ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ

аддитивные модели (баланс товарной продукции);

мультипликативные модели (двухфакторная модель, выражающая зависимость между объемом выпуска продукции, количеством единиц оборудования и выработкой продукции в расчете на одну единицу оборудования);

кратные модели (формула, которая выражает зависимость между продолжительностью оборота оборотных активов в днях, средней величиной этих активов за данный период и однодневным объемом продаж);

смешанные модели (показатель рентабельности активов, на уровень которого влияют три фактора: чистая прибыль, величина внеоборотных активов, величина оборотных активов).

Вначале необходимо построить экономико-математическую модель, которая будет описывать влияние отдельных факторов на обобщающие экономические показатели деятельности организации. В анализе хозяйственной деятельности большое распространение получили многофакторные мультипликативные модели, именно они позволяют изучить влияние значительного количества факторов на обобщающие показатели. Это поможет достичь большей глубины и точности анализа.

После построения экономико-математической модели необходимо выбрать способ её решения. Есть ряд традиционных способов: цепных подстановок, балансовый, абсолютных и относительных границ, индексный метод, а также методы корреляционно-регрессионного, кластерного, дисперсионного анализа. Но наряду с ними в экономическом анализе используются и специфически математические методы и способы. Одним их таких методов является интегральный. Он направлен на определение влияния отдельных факторов с использованием мультипликативных, кратных кратно-аддитивных моделей.

При применении интегрального метода имеется возможность получить более обоснованные результаты исчисления влияния отдельных факторов, чем при использовании метода цепных подстановок и его вариантов. Эти методы имеют следующий ряд недостатков:

Результаты расчетов влияния факторов зависят от принятой последовательности замены базисных величин отдельных факторов на фактические величины;

Дополнительный прирост обобщающего показателя, вызванный взаимодействием факторов, в виде неразложимого остатка присоединяется к сумме влияния последнего фактора

Если же использовать интегральный метод, то прирост делится поровну между всеми факторами.Интегральный метод устанавливает общий подход к решению моделей различных видов, независимо от числа элементов, которые входят в данную модель, и формы связи между этими элементами.

В основе интегрального метода факторного анализа лежит суммирование приращений функций, определенной как частная производная, умноженная на приращение аргумента на бесконечно малых промежутках. При применении интегрального метода необходимо соблюдать следующие условия:

должно соблюдаться условие непрерывной дифференцируемости функции, где в качестве аргумента берется какой-либо экономический показатель;

функция между начальной и конечной точками элементарного периода должна изменяться по прямой;

должно иметь место постоянство соотношений скоростей изменения величин факторов

При использовании интегрального метода исчисления определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования осуществляется по имеющейся стандартной программе с применением современных средств вычислительной техники.При осуществлении решения мультипликативной модели для расчета влияния отдельных факторов на обобщающий экономический показатель можно использовать следующие формулы:

При решении кратной модели для расчета влияния факторов воспользуемся формулами:

ΔZ(x) = Δx/Δy Ln y1/y0

Есть два основных типа задач, которые решаются при помощи интегрального метода: динамический и статистический. При статистическом отсутствует информация об изменении анализируемых факторов в течение данного периода. Примером такой задачи может быть анализ выполнения бизнес-планов либо анализ изменения экономических показателей по сравнению с предыдущим периодом. Динамический же тип задач имеет место в условиях наличия информации об изменении анализируемых факторов в течение данного периода. К такому типу задач можно отнести вычисления, связанные с изучением временных рядов экономических показателей.

Рассмотрим на примере преимущество интегрального метода.

Детерминированный факторный анализ

Для проведения детерминированного факторного анализа используют несколько моделей:

• кратную;
• адаптивную;
• мультипликативную.

В процессе осуществления вычислений при помощи каждой из них используют данные об исследуемых факторах, а также конечный результат.

Модель детерминированного факторного анализа	Формула	Расшифровка формулы
Кратная	А / А1	А, А1 – факторы
Адаптивная	А + А1 + А2 + … +Ан	А, А1, А2, Ан – факторы
Мультипликативная	А * А1 * А2 * … *Ан	А, А1, А2, Ан – факторы

То есть, детерминированный факторный анализ проводится путем нахождения частного от исследуемых факторов, их произведения или суммы.

Методы детерминированного факторного анализа

Детерминированный факторный анализ проводят при помощи следующих методов:

• цепных постановок;
• логарифмирования;
• абсолютных разниц;
• интегрального;
• относительных разниц.

Для получения достоверного результата, нужно тщательно отобрать факторы, которые непосредственно влияют на конечный результат деятельности.

Метод цепных постановок

Метод цепных подстановок представляет собой последовательную замену одного из показателей прошлого периода с отчетным. При этом все остальные факторы остаются нетронутыми. Изменяя показатель, необходимо проводить новый расчет.

Для анализа используют факторную модель:

ФМ = А * Б * В…Я,

где А, Б, В…Я – показатели, используемые в процессе.

Чтобы определить взаимосвязь между факторами и конечным результатом, необходимо найти разницу между результатами расчетов. Для этого из итога второго расчета нужно отнять результат первого, из третьего – второго, из четвертого – третьего и так далее

В процессе исследования важно соблюдать строгую последовательность, в противном случае, анализ может показать некорректную информацию

Метод логарифмирования

Метод логарифмирования считается одним из наиболее точных способов факторного анализа. Он заключается в составлении логарифма на основании показателей прошлого и отчетного периода.

Для этого находят сумму всех факторов, затем записывают алгебраическое выражение в виде произведения отношения фактических факторов к плановым. А уже на основании него составляют логарифм.

Метод абсолютных разниц

Основой для вычисления методом абсолютных разниц служит факторная модель:

ФМ = А * Б * В…Я,

где А, Б, В…Я – показатели, используемые в процессе.

Но для начала нужно найти абсолютные отклонения. Для этого из факторов базисного периода отнимают плановые показатели.

Для определения взаимосвязи между ними необходимо провести анализ при помощи факторной модели, заменяя относительные результаты на абсолютные отклонения.

Интегральный метод

Интегральный метод используется только тогда, когда конечный результат можно представить в виде функции от нескольких показателей. Интегральное выражение показывает зависимость функции от аргументов.

Метод относительных разниц

Метод относительных разниц используется для измерения влияния факторов на динамику конечного результата в мультипликативных и смешанных моделях. Он применяется в том случае, если данные для расчета выражены в относительных отклонения факторных показателей (процентах).

При проведении анализа данным методом за основу берется факторная модель:

ФМ = А * Б * В…Я,

где А, Б, В…Я – показатели, используемые в процессе.

Относительные отклонения находят по формуле:

(Аф – Ап) / Ап,

где Аф – фактический показатель;

Ап – плановый или базисный показатель.

Факторный анализ

Определение

Факторный анализ  – это процедура, с помощью которой большое число переменных, сводится к меньшему количеству независимых влияющих величин, называемых факторами. При этом в один фактор объединяются переменные (признаки), сильно коррелирующие (связанные) между собой. Переменные (признаки), относящиеся к разным факторам слабо коррелируют между собой.

Области применения факторного анализа

Факторный анализ используется при исследовании сложных объектов и систем (например, в психологии, биологии, социологии, экономике и др.) в том случае, когда напрямую невозможно измерять величины, определяющие свойства этих объектов (так называемые факторы). Однако для измерения доступны другие величины (переменные, признаки), которые зависят от этих факторов. Иными словами, фактор, который мы не можем измерить напрямую, проявляется в изменении нескольких переменных.

В области физической культуры и спорта в роли переменных могут выступать результаты тестирования уровня технической, физической, тактической подготовленности спортсменов, а также результаты медико-биологических и педагогических исследований.

Виды факторного анализа

Существует два основных вида факторного анализа – эксплораторный (исследовательский, разведочный) и конфирматорный (подтверждающий гипотезу).

Более подробно о методах статистической обработки данных рассказано в книгах:

• «Факторный анализ в педагогических исследованиях в области физической культуры и спорта»
• «Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта»
• «Компьютерная обработка данных экспериментальных исследований»

Эксплоаторный факторный анализ

Эксплораторный факторный анализ проводится на ранних этапах исследования, когда почти ничего не известно о структуре изучаемого явления и имеется значительное количество исходных данных. Цель проведения такого анализа – выявление латентной внутренней структуры и снижение размерности, то есть сокращение количества исследуемых переменных за счет объяснения их через новые факторные переменные. В ходе этого анализа, если необходимо, формулируются гипотезы, которые могут быть использованы для дальнейшего исследования.

Конфирматорный факторный анализ

Конфирматорный факторный анализ проводится для подтверждения уже выработанных гипотез. Этот вид факторного анализа  имеет строгие показатели и строгие критерии. Он предполагает, что уже выявлено какое-то количество факторов, необходимых для исследования и служит инструментом для проверки правильности выработанных гипотез, подтверждения выбранной структуры.  Изучаемые факторы тщательно продумываются и подбираются.

Исследователями в основном используется эксплораторный факторный анализ.

Бююль, А. SPSS: Искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей /А. Бююль, П. Цефель.– СПб: Диасофт.– СПб, 2001.– 608 с.
Дубров, А.М. Многомерные статистические методы для экономистов и инженеров /А.М. Дубров, В.С. Мхитарян, Л.И. Трошин /Учебн. для студ. эконом. специальностей ВУЗов.– М.: Финансы и статистика, 2000.
Дюк, В. Обработка данных на ПК в примерах / В. Дюк.– СПб: Питер, 1997. – 240 с.
Зациорский, В.М. Кибернетика, математика, спорт / В.М. Зациорский.– М.: Физкультура и спорт, 1969.–197 с.
Зациорский В

Осторожно: статистика! / В. Зациорский //Теория и практика физической культуры, 1989.– № 2.–С

52-55.
Ким, Дж.-О. Факторный анализ: статистические методы и практические вопросы / Дж.- О. Ким, Ч.У. Мьюллер // Факторный, дискриминантный и кластерный анализ / Пер.с англ. – М.: Финансы и статистика, 1989.– С. 5–74.
Масальгин, Н.А. Многомерный статистический анализ в исследованиях по физиологии спорта // Метод. разработка для аспирантов, преподавателей и слушателей Высшей школы тренеров и факультета усовершенствования / Н.А. Масальгин, А.С. Медведев.– М., 1991.– 35 с.
Самсонова, А.В. Факторный анализ. Направления применения и неиспользованные возможности /А.В. Самсонова //Вестник Балтийской Педагогической Академии.- 2005.- вып. 62.- С. 67-75
Самсонова, А.В. Факторный анализ в педагогических исследованиях в области физической культуры и спорта: учеб. пособие / А.В. Самсонова, И.Э. Барникова; Национальный государственный университет физической культуры, спорта и здоровья им. П.Ф. Лесгафта, Санкт-Петербург.– СПб.: , 2013. — 90 с.

3.4. Виды моделей. Моделирование

По характеру взаимосвязи между показателями различают методы детерминированного и стохастического факторного анализа.

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер.

Основные свойства детерминированного подхода к анализу:

1. построение детерминированной модели путем логического анализа;
2. наличие полной (жесткой) связи между показателями;
3. невозможность разделения результатов влияния одновременно действующих факторов, которые не поддаются объединению в одной модели;
4. изучение взаимосвязей в краткосрочном периоде.

Моделирование — процесс представления исследуемого показателя с факторами, которое передается в форме конкретного математического уравнения.

Различают четыре типа детерминированных моделей.

1. Аддитивные модели представляют собой алгебраическую сумму показателей и имеют вид:

К таким моделям, например, относятся показатели себестоимости во взаимосвязи с элементами затрат на производство и со статьями затрат; показатель объема производства продукции в его взаимосвязи с объемом выпуска отдельных изделий или объема выпуска в отдельных подразделениях.

2. Мультипликативные   модели   в   обобщенном   виде   могут быть представлены формулой:

Примером мультипликативной модели является двухфакторная модель объема производства продукции:

где Ч — среднесписочная численность работников;
CB — средняя выработка на одного работника.

3. Кратные модели:

Примером кратной модели служит показатель срока оборачиваемости товаров (в днях) Т_ОБ.Т:

где З_Т — средний запас товаров;О_Р — однодневный объем реализации.

4. Смешанные модели представляют собой комбинацию перечисленных выше моделей и могут быть описаны с помощью специальных выражений:

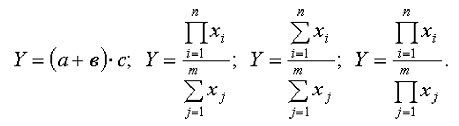
Примерами таких моделей служат показатели затрат на 1 руб. товарной продукции, показатели рентабельности и др.

Для изучения зависимости между показателями и количественного измерения множества факторов, повлиявших на результативный показатель, приведем общие правила преобразования моделей (моделирования) с целью включения новых факторных показателей.

Моделирование мультипликативных и аддитивных моделей осуществляется за счет разложения одного из факторных показателей на его сомножители:

A = a + b;                 b = c + d;                  A = a + c + d или

A = a * b;                   b = c * d;                   A = a * c * d

Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.

Кратные модели преобразуются следующими способами:

1. Удлинение.

.

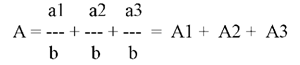
2. Формальное разложение.

b = b1 + b2 + b3

3. Расширение.

Для выделения некоторого числа новых факторов и построения необходимых для расчетов факторных показателей применяют прием расширения факторных моделей. При этом числитель и знаменатель умножаются на одно и тоже число.

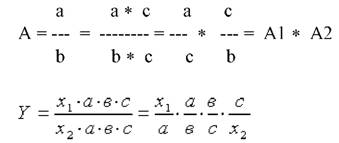
4. Сокращение.

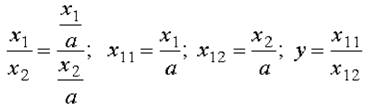
Для построения новых факторных показателей применяют прием сокращения факторных моделей. При использовании данного приема числитель и знаменатель делят на одно и то же число.

Процесс   моделирования   сложный   и   ответственный   момент. От реальности и точности моделей зависят конечные результаты анализа.

Детализация в факторном анализе во многом определяется числом факторов, влияние которых можно количественные оценить, поэтому большое значение в анализе имеют многофакторные мультипликативные модели.

В основе их построения лежат следующие принципы:

• место каждого фактора в модели должно соответствовать его роли в формировании результативного показателя;
• модель должна строиться из двухфакторной полной модели путем последовательного расчленения факторов, как правило качественных, на составляющие;
• при написании формулы многофакторной модели факторы должны располагаться слева направо в порядке их замены.

Построение факторной модели — первый этап детерминированного анализа. Далее определяют способ оценки влияния факторов.

Бальжинов А.В., Михеева Е.В. Анализ и диагностика финансово-хозяйственной деятельности предприятия: Учебн.пособ., — Улан-Удэ, 2003.

Поделиться
Добавить в закладки

Добавить комментарии