3 логические задачи, которые решат только самые сообразительные

Короткие загадки на логику друзьям

1. Какой пробкой нельзя заткнуть ни одну бутылку? (Ответ — дорожной)
2. В каком слове «нет» употребляется 100 раз? (Ответ — стонет)
3. Они бывают металлические и жидкие. О чем речь? (Ответ — гвозди)
4. По чему ходят часто, а ездят редко? (Ответ — по лестнице)
5. Как написать «уточка» в 2 клетках? (Ответ: В 1-ой — букву «у», во 2-ой — точку)
6. В каком слове 5 «е» и никаких других гласных? (Ответ — переселенец)
7. В каком слове «спрятался» напиток и природное явление? (Ответ — виноград)
8. Мальчик заплатил за бутылку с пробкой 11 рублей. Бутылка стоит на 10 рублей больше, чем пробка. Сколько стоит пробка? (Ответ — 50 копеек)
9. Отгадай загадку — у кого за носом пятка? (Ответ — обувь)
10. Больше часа, меньше минуты. (Ответ — секунда, стрелка некоторых моделей часов)
11. По какому пути еще никто никогда не ходил и не ездил? (Ответ — млечный путь)
12. В каком городе спрятались мужское имя и сторона света? (Ответ — Владивосток)
13. Перед каким простым смертным даже президент снимает шапку? (Ответ — парикмахер)
14. Какой стол не имеет ног? (Ответ — диетический)
15. Почему стоп-кран в поездах красного цвета, а в самолетах голубого? (Ответ — в самолетах нет стоп-крана.» На самом деле в самолете есть стоп-кран в кабине пилота)
16. По какому животному ходят люди и проезжают машины? (Ответ — зебра)
17. Завязать можно, а развязать нельзя. (Ответ — разговор)
18. Идет то в гору, то с горы, но остается на месте. (Ответ — дорога)
19. Какой слон без носа? (Ответ — шахматный)
20. Как человеку не спать 8 дней? (Ответ — спать по ночам)
21. У семерых братьев по сестре. Сколько всего сестер? (Ответ — одна)
22. Как может брошенное яйцо пролететь три метра и не разбиться? (Ответ — нужно бросить яйцо на четыре метра, тогда первые три метра оно пролетит целым)
23. Полтора судака стоят полтора рубля. Сколько стоят 13 судаков? (Ответ — 13 рублей)

На внимательность:

Пара лошадей пробежала 20 километров. Вопрос: сколько километров пробежала каждая лошадь в отдельности? (Ответ — 20 км)

На столе лежат две монеты, в сумме они дают 3 рубля. Одна из них — не 1 рубль. Какие это монеты? (Ответ — 1 и 2 рубля)

Вы вели автобус с 42 пассажирами из Бостона в Вашингтон. На каждой из шести остановок из него выходило по 3 человека, а на каждой второй — по четыре. Как звали водителя, когда водитель через 10 часов прибыл в Вашингтон? (Ответ — у водителя Ваше имя)

Логический тест – Test-help

Состоит из 5 вопросов, время на решение заданий – 5 минут. Здесь оценивается уровень пространственного мышления, прослеживается логика выбора варианта ответа. Принцип прохождения – даются последовательности графических задач, где нужно определить, куда поставить определенную картинку.

Очень интересная и занимательная методика для определения работы мыслительных процессов. Отлично подойдет как психодиагностический материал при приеме на работу. Можно проходить с ограничением по времени и без таймера. После ответа на последний вопрос нажмите кнопку “Завершить тестирование” – появятся результаты.

Мне понравился отчет по результатам – здесь есть ваши ответы, отображаются все правильные, а также рассчитывается ваша точность и относительный результат в процентах. По этому результату можно увидеть, насколько ваш результат отличается от ответов других участников, которые раньше отвечали на вопросы.

Задачи на логику по математике — подборка в стихах

Задачи на логику по математике — подборка в стихах

Задачи на логику по математике — подборка в стихах:

Упал орех у тропинки, Разбился на две половинки. Никак не поделят три ворона Две половинки поровну. Но тут — такая потеха! Упало еще два ореха И тоже на две половинки Разбились у той же тропинки. Теперь-то три черных ворона Добычу поделят поровну! Желаем им в этом успехов! Но каждому ворону, Ежели поровну, Сколько досталось орехов? Ответ: по одному ореху.

Три бельчонка маму-белку Ждали около дупла. Им на завтрак мама-белка Девять шишек принесла. Разделите на троих — Сколько каждому из них? Ответ: по три ореха.

Ежик по грибы пошел, Десять рыжиков нашел. Восемь положил в корзинку, Остальные же — на спинку. Сколько рыжиков везет На своих иголках еж? Ответ: 2 гриба

Мы на рынке были — Обувь всем купили. Для Анюты-лапочки Мы купили тапочки. Для Петра и Вовочки Взяли мы кроссовки. Туфли — для Антошки. Коле — босоножки. Босоножки — папе тоже. Маме — шлепанцы из кожи. Добрый выбрали товар. Посчитайте, сколько пар? Ответ: 7 пар.

У трехлетнего Андрюши Было лишь четыре груши. Слив было у Тараса Больше груш в четыре раза. У подружки, у Маринки, Десять персиков в корзинке. А у Валика с Лукой По антоновке одной. Сколько всех плодов подряд Было вместе у ребят? Ответ: 32 плода.

Плюсы и минусы, знаки деления, Равенства знаки и умножения, Всяких примеров, задач задается. Как же наука такая зовется?Ответ: Математика

Его вам надо пригласить, Чтоб равных чисел ряд сложить. Для облегчения сложения Есть знак отличный – …Ответ: Умножения

Два плюс два будет четыре, Какой знак можно поставить Между двойками, чтобы тоже Получилось 4?Ответ: Умножения

Арифметическое действие, Обратное сложению, Знак «минус» в нем задействован, Скажу вам, без сомнения.Ответ: Вычитание

Не все в этом действии гладко: То — целиком, а то — с остатком. В несколько раз уменьшение Выполнит вам — …Ответ: Деление

Прикатилось колесо, Ведь похожее оно, Как наглядная натура Лишь на круглую фигуру. Догадался, милый друг? Ну, конечно, это …Ответ: Круг

Он похожий на яйцо Или на твое лицо. Вот такая есть окружность — Очень странная наружность: Круг приплюснутым стал. Получился вдруг…Ответ: Овал

Три вершины тут видны, Три угла, три стороны, – Ну, пожалуй, и довольно! – Что ты видишь? – …Ответ: Треугольник

Четыре угла и четыре сторонки, Похожи точно родные сестренки. В ворота его не закатишь, как мяч, И он за тобою не пустится вскачь. Фигура знакома для многих ребят. Его вы узнали? Ведь это …Ответ: Квадрат

Два квадрата-близнеца – Половинки их отца. Сторонами приложи, Имя их отца скажи.Ответ: Прямоугольник

Чуть приплюснутый квадрат Приглашает опознать: Острый угол и тупой Вечно связаны судьбой. Догадались дело в чем? Как фигуру назовем?Ответ: Ромб

Каково мышление в 6-7 лет?

К 6 годам мозг ребенка уже настолько развит, что возникает новый качественный виток в развитии. Он способен воспринимать и обрабатывать даже сложные операции.

У детей значительно увеличивается словарный запас и развивается абстрактное мышление. Они без усилий переключаются с одного занятия на другое, при этом остаются внимательными и сконцентрированными. Мышление у них очень подвижное – в этом и состоит его особенность. Дети в этом возрасте уже осознанно устанавливают причинно-следственные взаимосвязи.

Однако самостоятельно развить свое логическое мышление ребенок не может. Родители должны суметь преподнести малышу идею занятий. Если сказать ребенку «сейчас мы начнем развивать твою логику сынок/дочка», результатов не будет. Для занятий нужна непринужденная обстановка, т.е. они должны проходить в виде игр.

Развитие обогатит представление ребенка об окружающем мире, даст понимание объединяющих закономерностей предметов и явлений, поможет объединять или выделять признаки предметов — общие и существенные.

Развитый ребенок в 6-7 лет должен уметь:

• самостоятельно продолжать логические ряды, без посторонних подсказок и наводящих вопросов;
• уметь найти лишний из 4-5 предложенных предметов;
• уметь составлять рассказы по картинкам с логическим завершением.

Задача №2

Давайте немного вспомним арифметические действия и применим их к задаче.

В кафе быстрого питания зашли четыре посетителя. При этом:

• первый посетитель купил три бургера и заплатил 300 рублей;
• второй посетитель купил один бургер и две порции картофеля фри и заплатил 200 рублей;
• третий посетитель купил два куска пиццы и одну порцию картофеля фри и заплатил 90 рублей;
• четвертый посетитель купил один бургер, одну порцию картофеля фри и один кусок пиццы.

Схематично эту ситуацию можно представить так:

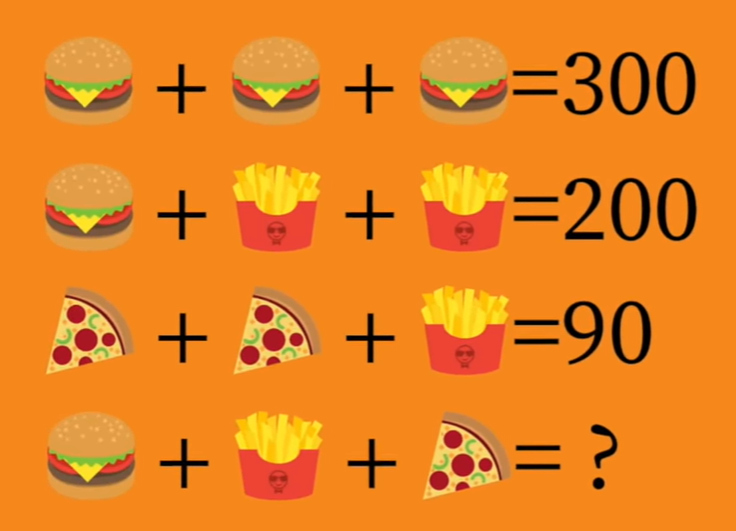
Вопрос: сколько заплатил четвертый посетитель?

Ответ

Если три бургера составили 300 рублей, то один бургер стоит 100 рублей (300/3). Если второй посетитель заплатил 100 рублей за бургер, то еще 100 рублей приходится на две порции картофеля, то есть одна порция картофеля фри стоит 50 рублей (100/2). Если третий посетитель заплатил 90 рублей, потратив 50 рублей на картофель, а сорок рублей на две пиццы, то одна пицца стоит 20 рублей (40/2). Соответственно четвертый посетитель заплатил: 100 + 50 + 20 = 170 рублей.

Геймификация

Геймификация (игрофикация) – термин лишь недавно пришедший с английского языка в русский. В самом широком понимании это – использование игровых подходов и игровой механики в неигровых ситуациях для повышения степени вовлеченности и решения поставленных задач. Методы геймификации стремятся воздействовать на естественные склонности человека к конкуренции, достижениям, самовыражению. Сегодня этот принцип широко распространен в маркетинге и онлайн торговле для привлечения и удержания клиентов.

Игрофикация учебного процесса является также прогрессивным направлением в образовании ХХІ века. Речь идет не только о классическом образовании, но и об обучающих программах повышения квалификации и онлайн курсах. Например, корпорация «Microsoft» выпустила игру «Ribbon Hero 2», как сопутствующий своему пакету офисных программ продукт. Игра была призвана помочь пользователям научиться эффективно использовать MS Office и стала одним из самых популярных проектов Microsoft Labs. «KhanAcademy», известный образовательный Интернет-портал, также широко практикует игры в своих программах. Не отстает и Нью-Йоркский департамент образования, который успешно реализует идею школы «Quest to Learn», где весь процесс обучения происходит с помощью игр.

В то же время, применение игр в процессе обучения чему-либо – не изобретение современности, хотя последняя и шагнула несколько вперед в этом отношении, значительно расширив возможности их применения. Еще в начале XVII века Я. А

Коменский обратил внимание на важность дидактической игры. Сегодня ученые располагают подтвержденными экспериментально сведениями о том, что практика обучения с привлечением логических и других игр на мышление способствует повышению интереса к предмету, росту продуктивности, активности и сообразительности. Но игра важна не только поэтому

Жизнь учит нас, что теория без практики ничего не стоит. По сути, игра как раз и предназначена для того, чтоб показать как «работает» знание и научить его применять

Но игра важна не только поэтому. Жизнь учит нас, что теория без практики ничего не стоит. По сути, игра как раз и предназначена для того, чтоб показать как «работает» знание и научить его применять.

Также нужно упомянуть и тот факт, что логические, психологические и другие игры важны не только в процессе обучения детей. Они широко применяются на тренингах, семинарах по повышению квалификации и эффективности для взрослых, поскольку позволяют сразу увидеть практическую пользу от полученных знаний. Используют игру и в других областях – многие работодатели, желая выявить лучших кандидатов при трудоустройстве, предлагают игровой конкурсный отбор, где нужно решить предложенный кейс (наиболее известный пример – корпорация Google Inc.). Даже в маленьких компаниях резюме зачастую проверяют и, чтобы выяснить наличие указанных аналитических способностей, HR-менеджер может предложить разгадать загадку или головоломку.

В это слабо верится, но взрослые часто не могут сделать то, с чем ребенок справляется за несколько минут. Поэтому, не только для профессионального развития, но и для саморазвития в целом, решение самых простых задачек на логику и мышление играет важную роль

Оно помогает отточить такие полезные навыки как память, внимание, устный счет, развить творческие способности

Законы логики

Существует 4 закона, знание которых позволяет лучше понять, что такое логика. Придерживаясь этих законов, можно гарантированно делать правильные и логичные умозаключения при условии наличия достаточного количества точно установленных фактов:

1. Закон тождества

Суть данного закона состоит в том, что суждение сохраняет своё предметное и смысловое значение в рамках одного контекста (например, в пределах одного логического рассуждения). Иными словами, недопустимо в процессе размышления подменять одно значение понятия или суждения другим, поскольку это приведёт к ложному выводу.

К примеру, утверждение «Выучить новый язык можно, общаясь с носителями на житейские темы» истинно в отношение английского или испанского языка, но слабо применимо к языкам программирования. Подобная подмена понятий является одним из грубых нарушений закона тождества. В данном примере она очевидна, но в некоторых случаях она используется как успешный демагогический приём.

2. Закон непротиворечия

Этот закон (называемый также «законом противоречия») гласит, что два высказывания, противоречащих друг другу, не могут быть истинными одновременно. Как минимум одно из них ложно. К примеру, если на столе лежит шар, полностью выкрашенный в один цвет, утверждения «Этот шар белый» и «Этот шар чёрный» не могут быть истинными одновременно. Но они оба вполне могут быть ложными, если шар, к примеру, красный.

Есть три основных типа логических противоречий:

1. Контактные. Это два несовместимых логических высказывания, следующих друг за другом.
2. Дистантные. Это взаимоисключающие высказывания, разделенные определенным интервалом.
3. Мнимые. Это кажущиеся противоречия, которых на самом деле нет, если понимать контекст, в котором делается утверждение (например, «Это красная смородина. А жёлтая она, потому что ещё зелёная»).

Контактные противоречия обычно не пытаются скрыть. Их используют сознательно, чтобы смягчить негативное высказывание («Ты хорошо справился, но это не совсем то, о чём я просил») или, наоборот, усилить его («Отлично! Ты опять всё испортил!»). Дистантные противоречия могут применять демагоги, чтобы запутать собеседника, но чаще их используют по ошибке неопытные или плохо подготовившиеся ораторы.

3. Закон исключённого третьего

Если одно суждение отрицает другое, то одно из них является ложным, а второе – истинным

Здесь важно не путать, что подразумевается под отрицанием

К примеру, утверждения «Этот шар белый» и «Этот шар чёрный» являются всего лишь взаимоисключающими. А отрицающими друг друга являются утверждения «Этот шар белый» и «Этот шар не белый» (одно из них обязательно является истинным, какого бы цвета ни был шар).

4. Закон достаточного основания

Этот закон ввёл Готфрид Лейбниц. Его суть состоит в том, что для того, чтобы считать утверждение истинным, необходимо располагать однозначными доказательствами, исключающими другие варианты. В повседневной жизни люди пренебрегают этим законом логики чаще, чем любым другим, делая однозначные выводы по косвенным фактам.

К примеру, если в середине лета вы несколько дней подряд не видели соседа, которого обычно встречаете ежедневно, можно предположить, что он уехал в отпуск. Скорее всего, так и есть, но всё же этот вывод противоречит закону достаточного основания, поскольку нельзя исключать, к примеру, болезнь или командировку.

Используйте комплексный подход

Среди всего многообразия логических задач часто дети выбирают себе пару любимых категорий и погружаются в их решение. Достаточно ли этого?

Наверняка большинство из нас хотя бы раз проходили тесты на уровень логики. Большинство их составлено из одних силлогизмов или вопросов с подвохом. Мы не предлагаем подобные тесты, потому что точно знаем, что определить уровень развития логического мышления с помощью десятка или двух вопросов, даже приблизительно, невозможно. Так же, как и развить нестандартное мышление, решая только отдельные типы логических задач.

Классические логические, комбинаторные и истинностные задачи, закономерности и математические ребусы, задачи про фигуры в пространстве и развертки, на перестановки и движение, на взвешивание и переливание; решаемые с конца, с помощью таблиц, отрезков, графов или кругов Эйлера – это далеко не все разнообразие логических задач, при решении которых активизируются всевозможные мыслительные операции и развивается творческое, нестандартное мышление.

Задачи на логику с подвохом — легкие

Задачи на логику с подвохом — легкие:

Задачи на логику с подвохом — легкие

ОТВЕТ: Если немножко подумать, то становится ясно, что каждая из пяти кошек ловит мышку для себя. А потому одному «пушистику» нужно ровно 5 минут, чтобы поймать желанную добычу.

Задачи на логику с подвохом — легкие

ОТВЕТ: Это имя на данный период времени является достаточно редким, поэтому мы практически его не слышим в быту. Женское имя с мягким знаком в конце — Любовь.

Задачи на логику с подвохом — легкие

ОТВЕТ: Мы привыкли к тому, что практически все вокруг нас имеет какую-то понятную для нас форму и размер. Но есть и то, что мы не можем идентифицировать по форме или размеру, но при этом у нас есть возможность быстрого и точного измерения определенных показателей. И говорим мы о времени и температуре.

Задачи на логику с подвохом — легкие

ОТВЕТ: Наверное, даже не стоит говорить о том, насколько все птички пугливы, поэтому если охотнику удалось подстрелить одну птичку, то все остальные вряд ли останутся сидеть на месте, они испугаются громкого звука и разлетятся в разные стороны. На дереве не останется ни одной птички.

Задачи на логику с подвохом — легкие

ОТВЕТ: Когда продавец закончил обслуживать глухонемого покупателя, он спросил у следующего стоящего в очереди, что его интересует. А так как человек не имел проблем с речью и слухом, то он отчетливо услышал вопрос и попросил дать ему ножницы.

Ответы на задачи

Задача 1

Ответ: 35 дней

Проще всего осознать данный ответ помогает визуальное восприятие через запись на бумаге прогрессий в обоих случаях (с одним и двумя «нулевыми» пациентами):

1 день — 1 больной;
2 день — 2 больных; 1 день — 2 больных;
3 день — 4 больных; 2 день — 4 больных;
4 день — 8 больных; 3 день — 8 больных;
5 день — 16 больных и т.д. 4 день — 16 больных и т.д.

То есть, если зараженных сразу было двое, то необходимо на один день меньше, чем было бы в случае с одним зараженным.

Задача 2

Ответ: 5 долларов

Естественно, мозг пытается подсказать очевидный и неправильный ответ – 10 долларов. Однако тогда получим цену планшета (на 100 долларов дороже стилуса) равной 110 долларам, а общая стоимость покупки тогда составит 110 + 10 = 120 долларов.

Задача 3

Ответ: $300 млрд

Проще всего решить эту задачу в лоб на бумаге, записав три простых уравнения вида: x + 200 = S, y + 140 = S и x + y = S — 40 и заменив одни переменные выражениями других.

Однако люди с гибким мышлением решают данную задачу более изящно:
Достаточно просто представить, что компания Google просто передала свои деньги на покупку Apple компании Microsoft. Последней не хватало изначально $140 млрд, а после получения денег Google стало не хватать всего 40$ млрд. Соответственно, компания Google располагала активом в размере $100 млрд и ей при этом не хватало 200 млрд для самостоятельной покупки Apple. Соответственно, цена Apple = $300 млрд.

Задача 4

Ответ: 3 минуты

Не составляет труда посчитать, что один 3D принтер печатает один треугольник за 3 минуты. Значит и 100 аппаратов произведут 100 единиц за те же 3 минуты.

Задача 5

Ответ: 40 ступенек

Подымаясь на 4 этаж, Коля преодолевает три лестничных пролета, соответственно, один лестничный пролет состоит из 120 / 3 = 40 ступенек. Поднимаясь на второй этаж, Петя проходит всего один пролет, то есть, 40 ступенек.

Как успеть на презентацию

Илон Маск, Билл Гейтс, Тим Кук и Марк Цукер­берг хотят пер­вы­ми попасть на пре­зен­та­цию Xiaomi, поэто­му реши­ли вый­ти ночью, что­бы к утру быть уже на месте. Кру­гом тем­но­та, без фона­ри­ка нико­му идти нель­зя, но он один на всех. Пре­зен­та­ция — на дру­гом бере­гу вели­кой реки Янц­зы. Мост через реку хлип­кий и может выдер­жать одно­вре­мен­но мак­си­мум дво­их. Как всем пере­брать­ся на дру­гой берег как мож­но скорее?

Ско­рость пере­хо­да моста у каж­до­го своя: про­вор­ный Илон Маск пере­хо­дит его за 1 мину­ту, бод­ря­щий­ся Билл Гейтс — за 2, спо­кой­ный Тим Кук — за 5. Марк Цукер­берг после слу­ша­ний в Кон­грес­се быст­ро ходить не может, поэто­му тра­тит на мост 10 минут. Когда мост пере­хо­дят два чело­ве­ка, их ско­рость рав­на ско­ро­сти само­го мед­лен­но­го из пары.

Зада­ча — пере­ве­сти геро­ев на дру­гой берег как мож­но ско­рее, ведь места в оче­ре­ди у конгресс-центра уже зани­ма­ют мест­ные жители.

Решение

Самая ско­рост­ная пара у нас — Маск и Гейтс, поэто­му они с фона­ри­ком пере­хо­дят на дру­гой берег за 2 мину­ты (ско­рость Гейтса):

Илон Маск (1) и Билл Гейтс (2) → пере­шли на тот берег за 2 минуты.

Отправ­ля­ем с фона­рём назад само­го быст­ро­го из них:

Илон Маск (1) → вер­нул­ся обрат­но с фона­рём за 1 минуту.

Теперь нуж­но решить, какая пара пой­дёт сле­ду­ю­щей. Так как нам в любом слу­чае нуж­но отправ­лять Цукер­бер­га на тот берег, то это гаран­ти­ро­ван­но зай­мёт дол­гих 10 минут. Что­бы исполь­зо­вать это вре­мя опти­маль­но, отпра­вим с ним Тима Кука, кото­рый тоже не самый быст­рый из всех:

Тим Кук (5) и Марк Цукер­берг (10) → пере­шли на тот берег за 10 минут.

Оста­лось забрать Ило­на Мас­ка с того бере­га, зна­чит посы­ла­ем за ним само­го быст­ро­го из доступ­ных — Бил­ла Гейтса:

Билл Гейтс (2) → вер­нул­ся обрат­но с фона­рём за 2 минуты.

И они вдво­ём с Мас­ком отправ­ля­ют­ся на тот берег:

Илон Маск (1) и Билл Гейтс (2) → пере­шли на тот берег за 2 минуты.

Скла­ды­ва­ем все мину­ты на мосту: 2 + 1 + 10 + 2 + 2 = 17 минут. Зна­чит, все­го 17 минут им потре­бу­ет­ся, что­бы перей­ти вели­кую реку Янц­зы и занять места в зале рань­ше всех.

Монти Холл и три шкатулки

Перед вами сто­ят три оди­на­ко­вых закры­тых шка­тул­ки, в одной из них лежит мно­го денег, а две дру­гих — пустые. Мож­но выбрать любую шка­тул­ку, но сра­зу откры­вать нель­зя. Затем веду­щий игры берёт одну из остав­ших­ся шка­ту­лок, откры­ва­ет и пока­зы­ва­ет, что она пустая.

Теперь у вас есть выбор: оста­вить себе ту шка­тул­ку, кото­рую вы выбра­ли с само­го нача­ла, или поме­нять её на остав­шу­ю­ся неот­кры­тую. Как луч­ше поступить?

Решение

Отбро­сим в сто­ро­ну эмо­ции, инту­и­цию и про­чую эзо­те­ри­ку и нач­нём решать эту зада­чу как про­грам­ми­сты — дадим нашим шка­тул­кам имена:

• Выбран­ная — шка­тул­ка, кото­рую мы выбра­ли с само­го начала;
• Пустая — ту, кото­рую откры­ли после наше­го выбо­ра и пока­за­ли, что она пустая;
• Неиз­вест­ная — одна из двух невы­бран­ных нами шка­ту­лок, кото­рая оста­лась закры­той, и на кото­рую мож­но поме­нять нашу.

Изна­чаль­но веро­ят­ность того, что вы выбра­ли сра­зу шка­тул­ку с день­га­ми — 33%, пото­му что в самом нача­ле у каж­дой шка­тул­ки оди­на­ко­вые шан­сы. Но теперь всё зави­сит от того, слу­чай­но ли веду­щий открыл Пустую шка­тул­ку, или знал зара­нее, что в ней ниче­го нет. Имен­но от это­го будет зави­сеть, как нуж­но поступить.

Если пустую шкатулку открыли случайно

Допу­стим, веду­щий игры не знал ниче­го о содер­жа­нии шка­тул­ки. То есть, откры­вая одну из невы­бран­ных, он мог открыть и шка­тул­ку с деньгами.

Раз это­го не про­изо­шло и никто дей­стви­тель­но зара­нее не знал, в какой из шка­ту­лок день­ги, то у них теперь рав­ные шан­сы на побе­ду: вме­сто ⅓ они ста­ли рав­ны ½. У обе­их шка­ту­лок теперь оди­на­ко­вая веро­ят­ность ока­зать­ся с день­га­ми, поэто­му менять шка­тул­ки смыс­ла нет: мате­ма­ти­че­ски это никак не уве­ли­чит ваши шан­сы. Всё, что будет даль­ше, уже эзотерика.

Ито­го. Если Пустую шка­тул­ку откры­ли слу­чай­но и никто не знал зара­нее, что она пустая, то вер­ная стра­те­гия будет такой: оста­вить себе Выбран­ную шкатулку.

Пустую шкатулку выбрали специально

Теперь рас­смот­рим ситу­а­цию: веду­щий знал, что откры­тая шка­тул­ка ока­жет­ся пустой. Он изна­чаль­но знал, где лежат день­ги, и спе­ци­аль­но выбрал пустую шка­тул­ку, что­бы её открыть. Это совсем дру­гая ситу­а­ция, хотя может пока­зать­ся, что она такая же, как и в пер­вом слу­чае. На самом деле нет. Там у нас появ­ля­лась новая инфор­ма­ция, пото­му что никто не знал, где лежат день­ги. Новая инфор­ма­ция заста­ви­ла пере­счи­тать шансы.

В этом слу­чае новой инфор­ма­ции нет, пото­му что шка­тул­ка с день­га­ми извест­на зара­нее. А раз новой инфор­ма­ции нет, то у Выбран­ной шка­тул­ки, шан­сы на побе­ду как были ⅓, так и оста­лись. А теперь начи­на­ет­ся магия тео­рии веро­ят­но­сти: шан­сы на побе­ду у Неиз­вест­ной шка­тул­ки вырос­ли вдвое!

Дело тут вот в чём. Раз изна­чаль­но у всех шка­ту­лок шан­сы были рав­ны, то для каж­дой шка­тул­ки они состав­ля­ли ⅓. Когда нам умыш­лен­но откры­ли Пустую шка­тул­ку, то веро­ят­ность Выбран­ной шка­тул­ки не поме­ня­лась (так как новой инфор­ма­ции нет), а веро­ят­ность Неиз­вест­ной шка­тул­ки вырос­ла вдвое:

⅓, кото­рая была изна­чаль­но + ⅓, кото­рая пере­шла от Пустой шка­тул­ки к Неиз­вест­ной = ⅔.

Нет новой инфор­ма­ции — шан­сы не пере­счи­ты­ва­ют­ся, а пере­рас­пре­де­ля­ют­ся меж­ду теми шка­тул­ка­ми, содер­жи­мое кото­рых зара­нее извест­но. Раз откры­ва­ю­щий шка­тул­ки зна­ет, где день­ги, зна­чит, шан­сы пере­рас­пре­де­ля­ют­ся меж­ду ними. А у вашей шка­тул­ки как был шанс на побе­ду ⅓, так и остался.

Ито­го. Если Пустую шка­тул­ку откры­ли спе­ци­аль­но, пра­виль­ная стра­те­гия будет такой: поме­нять Выбран­ную шка­тул­ку на Неиз­вест­ную. Это повы­сит ваши шан­сы на побе­ду в 2 раза. 

Трудные загадки на логику

1. Где на Земле дует всегда южный ветер? (Ответ — на Северном полюсе)
2. Что станет больше, если его перевернуть вверх ногами? (Ответ — число 6)
3. Где люди платят за то, что у них отнимают? (Ответ — парикмахерская)
4. Из какого крана нельзя помыть руки? (Ответ — из строительного)
5. Человек скупал фрукты по 10 рублей за штуку, но продавал их по 5 рубля за штуку. Спустя какое-то время он стал миллионером. Как у него это получилось? (Ответ — он был миллиардером)
6. Какой остров сам себя называет предметом белья? (Ответ — Ямайка, я — майка)
7. Детей у него может и не быть, но он все равно папа. Как такое возможно? (Ответ — это Папа Римский)
8. Какую маленькую лошадку нужно поставить между двумя местоимениями, чтобы получилось название страны? (Ответ — пони, Япония)
9. На столе лежит 100 листов бумаги. За каждые 10 секунд можно посчитать 10 листов. Сколько секунд понадобится, чтобы посчитать 80 листов? (Ответ — 80 секунд)
10. Какой человек сможет удержать слона? (Ответ- шахматист)
11. Союз, число потом предлог — вот и вся загадка. А чтоб ответ найти ты смог, о реках вспомнить надо. (Ответ — исток)
12. Человек полностью здоров, не умер, не инвалид, но выносят его из больницы на руках. (Ответ — новорожденный)
13. Жители средневековой Европы иногда привязывали к подошвам деревянные чурки. С какой целью они это делали? (Ответ — для защиты от грязи, так как канализации не было и помои выливали прямо на улицу)
14. Банка стоит на столе. Стоит она так, что одна ее половина находится в воздухе, а другая на столе. Что лежит в банке, если через полчаса она упадет? И почему? (Ответ — лед. Он растает, и банка упадет)
15. Ночной сторож умер днем. Дадут ли ему пенсию? (Ответ — мертвому пенсия не дают)
16. Можно ли с помощью сети ловить воду? (Ответ — можно, если вода замерзла)
17. Сколько различных цифр надо использовать, чтобы написать число 100? (Ответ — две, ноль и один)
18. В месяце три воскресенья выпали на четные числа. Какой день недели был седьмого числа этого месяца? (Ответ: пятница. Воскресенья выпадут на числа: 2, 9, 16, 23, 30)
19. Разутый, но в сапогах. Ходит по земле, но вниз головой. (Ответ — гвоздь в сапоге)
20. Что можно взять в левую руку, но нельзя в правую? (Ответ — локоть правой руки)
21. Собака была привязана к десятиметровой верёвке, а прошла 300 метров. Как ей это удалось? (Ответ — верёвка была ни к чему не привязана)
22. Мужчина вёл большой грузовик. Огни на машине не были зажжены. Луны тоже не было. Женщина стала переходить дорогу перед машиной. Как удалось водителю разглядеть её? (Ответ — был яркий солнечный день)
23. Если пять кошек ловят пять мышей за пять минут, то сколько времени нужно одной кошке, чтобы поймать одну мышку? (Ответ — пять минут)
24. Можно ли зажечь спичку под водой? (Ответ — можно, если воду налить в какую-то ёмкость, например, в стакан, а спичку держать ниже стакана)
25. Как разделить пять яблок между пятью мальчиками так, чтобы каждый получил по яблоку и при этом одно из яблок осталось в корзинке? (Ответ — отдать одному мальчику яблоко вместе с корзинкой)

Сбиваем с толку:

Можно ли предсказать счет футбольного матча до его начала и если да, то как? (Ответ — счёт любого матча до его начала всегда 0:0)

Пять машин текстильной фабрики производят пять вещей за пять минут. За сколько минут 100 машин изготовят 100 вещей? (Ответ — за 5 минут)

На озере растут кувшинки. Каждый день их количество увеличивается в два раза. Известно, что кувшинки полностью покроют всю поверхность озера за 48 дней. Сколько дней потребуется кувшинкам, чтобы покрыть половину озера? (Ответ — 47 дней)

Странный разговор двух программистов

Встре­ча­ют­ся два про­грам­ми­ста, кото­рые дав­но друг дру­га не виде­ли. У них про­ис­хо­дит такой диалог:

— Я слы­шал, у тебя дети появились.

— Да, три сына.

— И сколь­ко им лет?

— Ну… В сум­ме — тринадцать!

— Хм… Ты сно­ва загад­ка­ми гово­ришь? Ну лад­но. Что ещё можешь сказать?

— Если воз­рас­ты пере­мно­жить, полу­чит­ся столь­ко же, сколь­ко окон вон у того дома.

Про­грам­мист счи­та­ет окна и при­ки­ды­ва­ет варианты. 

— Но это­го до сих пор недо­ста­точ­но для ответа!

— Могу доба­вить, что мой стар­ший сын — рыжий.

— Ну теперь совсем дру­гое дело. Им … (далее сле­ду­ет ответ).

— Пра­виль­но!

Сколь­ко же лет им было? И как пер­вый смог вычис­лить возраст?

Решение

Если вам до сих пор кажет­ся, что эта зада­ча — пол­ная дичь, мы вас пони­ма­ем. И всё-таки у неё есть чёт­кое, логич­ное и точ­ное решение.

Суть его в том, что каж­дый ответ вто­ро­го — уточ­не­ние или под­сказ­ка для реше­ния. И пер­вый зада­вал вопро­сы до тех пор, пока все под­сказ­ки не при­ве­ли его к пра­виль­но­му отве­ту. Давай­те про­сле­дим за ходом его мыслей.

Пер­вый ответ гово­рит нам о том, что все­го детей — трое. Хоро­шо, но явно недо­ста­точ­но для того, что­бы вычис­лить возраст.

Вто­рой ответ гово­рит о том, что в сум­ме детям 13 лет. Давай­те запи­шем все воз­мож­ные ком­би­на­ции воз­рас­тов, кото­рые под­хо­дят под это условие:

1 + 1 + 11 = 13

1 + 2 + 10 = 13

1 + 3 + 9 = 13

1 + 4 + 8 = 13

1 + 5 + 7 = 13

1 + 6 + 6 = 13

2 + 2 + 9 = 13

2 + 3 + 8 = 13

2 + 4 + 7 = 13

2 + 5 + 6 = 13

3 + 3 + 7 = 13

3 + 4 + 6 = 13

3 + 5 + 5 = 13

4 + 4 + 5 = 13

Осталь­ные ком­би­на­ции полу­ча­ют­ся из этих про­стой пере­ста­нов­кой возрастов.

Тре­тий ответ — про­из­ве­де­ние воз­рас­тов рав­но чис­лу окон. Кажет­ся, что это вооб­ще никак нам не помо­га­ет, пото­му что мы не зна­ем коли­че­ства окон в доме, — но это не так. Если бы это­го отве­та было доста­точ­но, то пер­вый бы сра­зу назвал воз­раст, но раз он это­го не сде­лал, зна­чит, инфор­ма­ции было недостаточно.

Давай­те посмот­рим на про­из­ве­де­ния всех ком­би­на­ций воз­рас­тов и попро­бу­ем понять, что же с ними не так:

1 × 1 × 11 = 11

1 × 2 × 10 = 20

1 × 3 × 9 = 27

1 × 4 × 8 = 32

1 × 5 × 7 = 35

1 × 6 × 6 = 36

2 × 2 × 9 = 36

2 × 3 × 8 = 48

2 × 4 × 7 = 56

2 × 5 × 6 = 60

3 × 3 × 7 = 63

3 × 4 × 6 = 72

3 × 5 × 5 = 75

4 × 4 × 5 = 80

Раз это­го отве­та про коли­че­ство окон ока­за­лось недо­ста­точ­но, зна­чит в доме было столь­ко окон, что под это чис­ло попа­да­ли сра­зу несколь­ко резуль­та­тов про­из­ве­де­ний. Мы выде­ли­ли их в таб­ли­це. Все осталь­ные чис­ла дава­ли бы одно­знач­ный ответ про воз­раст, а для чис­ла 36 есть несколь­ко вари­ан­тов, поэто­му пер­вый ска­зал, что это­го ему недостаточно.

Чет­вёр­тый ответ — стар­ший сын рыжий. Цвет волос нам не так важен, как коли­че­ство стар­ших сыно­вей. Так как «стар­ший сын» озна­ча­ет, что он такой стар­ший один, зна­чит, вари­ант 1 — 6 — 6 нам не под­хо­дит, пото­му что в нём стар­ших сыно­вей двое. Оста­ёт­ся толь­ко один вари­ант: 2 — 2 — 9.

Ответ: стар­ше­му сыну 9 лет, двум дру­гим — по 2 года.